题目内容
【题目】定义:两直角边比为1:2的直角三角形叫做和合三角形.
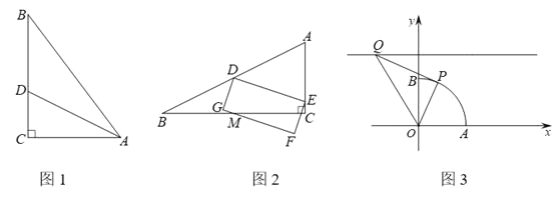
(1)如图1,△ABC中,∠C= ![]() ,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;
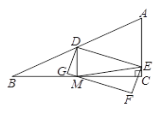
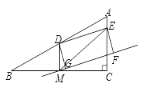
(2)如图2,和合△ABC中,∠C= ![]() ,AC=
,AC= ![]() ,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;
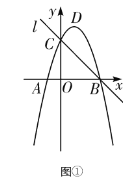
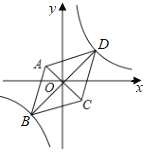
(3)如图3,扇形OAB中,∠AOB= ![]() ,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是
,OA=2.以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是 ![]() 一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
一动点,点Q是直线y=3上一动点,当△OPQ是和合三角形时,求点P坐标.
【答案】(1)证明见解析;(2)2;(3)P  ,
, 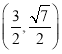
【解析】
(1)过点D作DE⊥AB,易证Rt△ACD≌Rt△AED,所以AE=AC=3,所以BE=2,设CD=x,则DE=x,DB=4-x,在Rt△BDE中,![]() ,列出方程式可求得
,列出方程式可求得![]() ,则CD∶AC=1∶2,即证△ACD是和合三角形;
,则CD∶AC=1∶2,即证△ACD是和合三角形;
(2)易证DM∥AC,且DM= ![]() AC,由三角形面积关系可得S△DME=
AC,由三角形面积关系可得S△DME= ![]() S△ABC,因为S△DME=
S△ABC,因为S△DME= ![]() DEEF=
DEEF= ![]() S矩形DEFG,即可求得S矩形DEFG=
S矩形DEFG,即可求得S矩形DEFG= ![]() S△ABC=2;
S△ABC=2;
(3)分三种情况讨论即可,分别讨论△OPQ中三个内角为90°时,点P的坐标即可.
(1)解:过点D作DE⊥AB
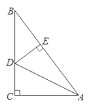
∵AD平分∠CAB,∠C= ![]()
∴DE=CD
∵AD=AD
∴Rt△ACD≌Rt△AED
∴AE=AC=3
在Rt△ABC中,AC=3,BC=4,
∴AB=5
∴BE=2
设CD=x,则DE=x,DB=4-x
在Rt△BDE中,![]()
即:![]()
解得:![]()
∴CD∶AC=1∶2
∴△ACD是和合三角形;
(2)解:∵点D是边AB中点,点M是边BC中点
∴DM∥AC,且DM= ![]() AC
AC
∴S△DME= ![]() ×DM×MC=
×DM×MC= ![]() =
= ![]() =
= ![]() S△ABC
S△ABC
∵S△DME= ![]() ×DE×EF=
×DE×EF= ![]() S矩形DEFG
S矩形DEFG
∴S矩形DEFG= ![]() S△ABC=2;
S△ABC=2;
(3)解:①∵ ![]()
∴ ![]()
②当 ![]() 时
时
过点P作CD⊥x轴于点D,交直线y=3于点C
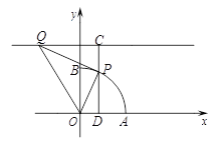
则 ![]()
∴ ![]()
∵ ![]()
∴ ![]()
∴ ![]()
∴△OPD∽△PQC
∴ ![]() 或
或 ![]()
设OD=a,则CP=2a或![]()
∴PD=3-2a或3-![]()
在Rt△OPD中,![]()
若PD=3-2a
则 ![]()
解得: ![]() (舍去),
(舍去), ![]()
若PD=3-![]()
则 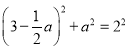
方程无解
∴点P 
③当 ![]() 时
时
分别过点P,Q作PE⊥x轴于点E,QF⊥x轴于点F
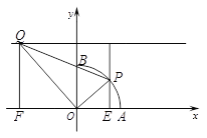
同②理:△OPE∽△QOF
∴ ![]() 或
或 ![]()
∵ ![]()
∴OE=6(舍去),或OE= ![]()
∴PE= ![]()
∴点P 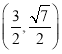
综上,点P  ,
, 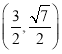 .
.

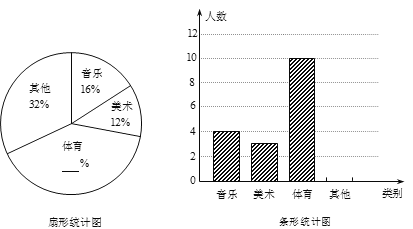
【题目】某学校为了了解九年级学生上学期间平均每天的睡眠情况,现从全校![]() 名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间
名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间![]() (单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
(单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
平均每天睡眠时间分组统计表
组别序号 | 睡眠时间 | 人数(频数) |
|
|
|
|
|
|
|
|
|
|
|
|
平均每天睡眠时间扇形统计表
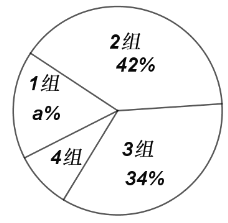
(1)![]() _______,
_______,![]() _______,
_______,![]() _______(
_______(![]() 为百分号前的数字);
为百分号前的数字);
(2)随机抽取的这部分学生平均每天睡眠时间的中位数落在_______组(填组别序号);
(3)估计全校![]() 名九年级学生中平均每天睡眠时间不低于
名九年级学生中平均每天睡眠时间不低于![]() 小时的学生有_______名;
小时的学生有_______名;
(4)若所抽查的睡眠时间![]() (小时)的
(小时)的![]() 名学生,其中
名学生,其中![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加个别访谈,请用列表或画树状图的方法求选取的
名学生参加个别访谈,请用列表或画树状图的方法求选取的![]() 名学生恰为
名学生恰为![]() 男
男![]() 女的概率.
女的概率.