题目内容
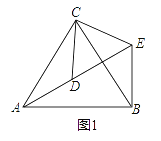
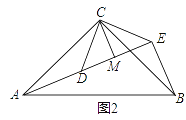
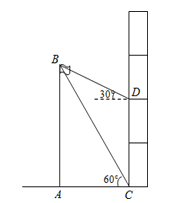
【题目】某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为
A.9米B.6![]() 米C.6米D.(6+
米C.6米D.(6+![]() )米
)米
【答案】A
【解析】
过点D作DE⊥AB,垂足为E,则四边形ACDE为矩形,AE=CD=6米,AC=DE.设BE=x米,先解Rt△BDE,得出DE=![]() x米,AC=
x米,AC=![]() x米,再解Rt△ABC,得出AB=3x米,然后根据AB-BE=AE,列出关于x的方程,解方程即可.
x米,再解Rt△ABC,得出AB=3x米,然后根据AB-BE=AE,列出关于x的方程,解方程即可.
过点D作DE⊥AB,垂足为E,由题意可知,四边形ACDE为矩形,
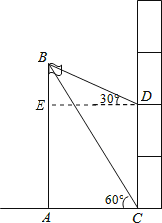
则AE=CD=6米,AC=DE.
设BE=x米.
在Rt△BDE中,∵∠BED=90°,∠BDE=30°,
∴DE=![]() BE=
BE=![]() x米,
x米,
∴AC=DE=![]() x米.
x米.
在Rt△ABC中,∵∠BAC=90°,∠ACB=60°,
∴AB=![]() AC=
AC=![]() ×
×![]() x=3x米,
x=3x米,
∵AB-BE=AE,
∴3x-x=6,
∴x=3,
AB=3×3=9(米).
即旗杆AB的高度为9米.
故选A.

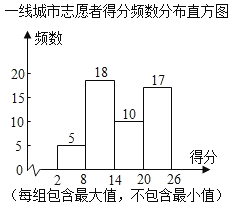
【题目】为了解疫情对精神负荷造成的影响,某机构分别在一线城市和三线城市的志愿者中随机选取了50人参加LES测试,根据志愿者的答题情况计算出LES得分,并对得分进行整理,描述和分析,部分信息如下:
一、三线城市志愿者得分统计表
城市 | 中位数 | 平均数 |
一线城市 | a | 17.6 |
三线城市 | 14 | 17.2 |
注:一线城市在14<x≤20中的得分是:15,15,16,17,17,17,17,18,18,20.
根据以上信息,解答下列问题:
(1)表中a的值为 ;
(2)得分越低反映个体承受的精神压力越小,排名越靠前,在这次调查中,一线城市的志愿者甲和三线城市的志愿者乙的得分均为15分,请判断甲、乙在各自城市选取的志愿者中得分排名谁更靠前,并说明理由;
(3)如果得分超过平均数就需要进行心理干预,请估计一线城市全部2000名志愿者中有多少人需要进行心理干预?