题目内容
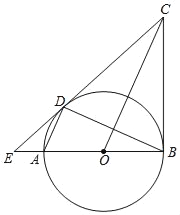
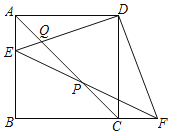
【题目】如图,在边长为4的正方形ABCD中,∠EDF=90°,点E在边AB上且不与点A重合,点F在边BC的延长线上,DE交AC于Q,连接EF交AC于P
(1)求证:△ADE≌△CDF;
(2)求证:PE=PF;
(3)当AE=1时,求PQ的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据ASA证明即可.
(2)作FH∥AB交AC的延长线于H,由“AAS”可证△APE≌△HPF,可得PE=PF;
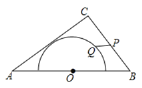
(3)如图2,先根据平行线分线段成比例定理表示![]() ,可得AQ的长,再计算AH的长,根据(2)中的全等可得AP=PH,由线段的差可得结论.
,可得AQ的长,再计算AH的长,根据(2)中的全等可得AP=PH,由线段的差可得结论.
(1)证明:∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠BCD=∠DCF=∠ADC=90°,
∴∠ADE+∠EDC=90°
∵∠EDF=90°
∴∠EDC+∠CDF=90°
∴∠ADE=∠CDF
在△ADE和△CDF中,
∵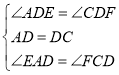
∴△ADE≌△CDF(ASA).
(2)证明:由(1)知:△ADE≌△CDF,
∴AE=CF,
作FH∥AB交AC的延长线于H.
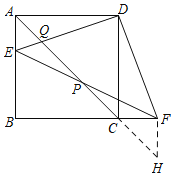
∵四边形ABCD是正方形,
∴∠ACB=∠FCH=45°,
∵AB∥FH,
∴∠HFC=∠ABC=90°,
∴∠FCH=∠H=45°,
∴CF=FH=AE,
在△AEP和△HFP中,
∵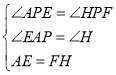 ,
,
∴△APE≌△HPF(AAS),
∴PE=PF;
(3)∵AE∥CD,
∴![]() ,
,
∵AE=1,CD=4,
∴![]() ,
,
∵四边形ABCD是正方形,
∴AB=BC=4,∠B=90°,
∴AC=4![]() ,
,
∴AQ=![]() AC=
AC=![]() ,
,
∵AE=FH=CF=1,
∴CH=![]() ,
,
∴AH=AC+CH=4![]() +
+![]() =5
=5![]() ,
,
由(2)可知:△APE≌△HPF,
∴AP=PH,
∴AP=![]() AH=
AH=![]() ,
,
∴PQ=AP﹣AQ=![]() ﹣
﹣![]() =
=![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目