题目内容
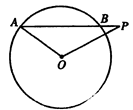
如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP=___________.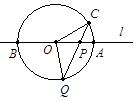

40°
点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
解答: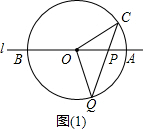 解:①根据题意,画出图(1),
解:①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
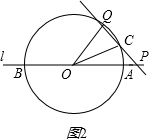
②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°-∠QOC)×1/2①,
∵OQ=PQ,
∴∠OPQ=(180°-∠OQP)×1/2②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得:
60°+∠QOC=∠OQP,
∵∠OQP=∠QCO,
∴∠QOC+2∠OQP=∠QOC+2(60°+∠QOC)=180°,
∴∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;

③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°-∠COQ)×1/2①,
∵OQ=PQ,
∴∠P=(180°-∠OQP)×1/2②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°-150°-10°=20°.
故答案为:40°、20°、100°.
解答:
 解:①根据题意,画出图(1),
解:①根据题意,画出图(1),在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.

②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°-∠QOC)×1/2①,
∵OQ=PQ,
∴∠OPQ=(180°-∠OQP)×1/2②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得:
60°+∠QOC=∠OQP,
∵∠OQP=∠QCO,
∴∠QOC+2∠OQP=∠QOC+2(60°+∠QOC)=180°,
∴∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;

③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°-∠COQ)×1/2①,
∵OQ=PQ,
∴∠P=(180°-∠OQP)×1/2②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°-150°-10°=20°.
故答案为:40°、20°、100°.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 cm2,则这个圆锥的高为 ▲cm.
cm2,则这个圆锥的高为 ▲cm.



 +
+
 于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):(6分)
于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):(6分)
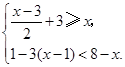
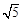 .求⊙O1的半径.
.求⊙O1的半径.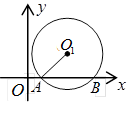
 解答下列问题:(各小问结果保留π)
解答下列问题:(各小问结果保留π)