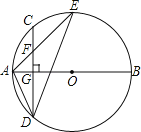
��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У����ڵ�![]() �͵�
�͵�![]() �������¶��壺��
�������¶��壺��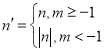 ����Ƶ�
����Ƶ�![]() Ϊ��
Ϊ��![]() �ľ��Ե㣮���磺��
�ľ��Ե㣮���磺��![]() �ľ��Ե�������
�ľ��Ե�������![]() ����
����![]() �ľ��Ե�������
�ľ��Ե�������![]() ��
��
��1����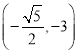 �ľ��Ե�������_______��
�ľ��Ե�������_______��
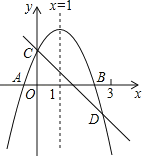
��2������![]() �ں���
�ں���![]()
![]() ��ͼ���ϣ�����Ե�
��ͼ���ϣ�����Ե�![]() ��������
��������![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3������![]() �ڹ���
�ڹ���![]() �Ķ��κ���
�Ķ��κ���![]() ͼ���ϣ�����Ե�
ͼ���ϣ�����Ե�![]() ��������
��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��![]() ������
������![]() ����
����![]() ���Ƿ����
���Ƿ����![]() ʹ��
ʹ��![]() �����ֵ�����������
�����ֵ�����������![]() �����ֵ����ʱ
�����ֵ����ʱ![]() ��ֵ�����ޣ���˵�����ɣ�
��ֵ�����ޣ���˵�����ɣ�
���𰸡���1��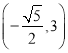 ����2��3��k��5����3�����ڣ���t=-
����2��3��k��5����3�����ڣ���t=-![]() ʱ��Sȡ�����ֵ
ʱ��Sȡ�����ֵ![]() ��
��
��������
��1�����ݸ����Ķ����ֱ�ӵó������
��2�����������֪y=x-1��-3��x��k��k��-3����ͼ���ϵĵ�P�ľ��Ե�Q���ں���![]() ��ͼ���ϣ����ͼ�ɵõ��𰸣�
��ͼ���ϣ����ͼ�ɵõ��𰸣�
��3���������![]() �Ķ������꣬��������ͼ���ϵĵ�P�ľ��Ե�Q���ں���n����
�Ķ������꣬��������ͼ���ϵĵ�P�ľ��Ե�Q���ں���n����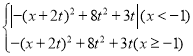 ��ͼ���ϣ����-2t��-1�Ĺ�ϵȷ��y����ֵ��������a��b��ʾ��s������t��ȡֵ��Χ���s��ȡֵ��Χ��
��ͼ���ϣ����-2t��-1�Ĺ�ϵȷ��y����ֵ��������a��b��ʾ��s������t��ȡֵ��Χ���s��ȡֵ��Χ��
�⣺��1�������¶��壬
��![]() ��-1�����
��-1�����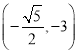 �ľ��Ե�������
�ľ��Ե�������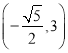 ��
��
�ʴ�Ϊ��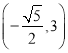 ��
��
��2�������⣬y=x-1��-3��x��k��k��-3��ͼ���ϵĵ�P�ľ��Ե�Q���ں���n��=![]() ��ͼ���ϣ���ͼ1����
��ͼ���ϣ���ͼ1����
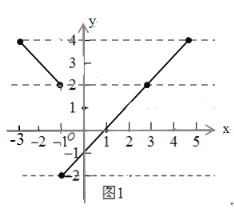
��x=-1ʱ��n��ȡ��Сֵ��n��=-1-1=-2��
��n��=4ʱ��x-1=4��1-x=4����x=5��x=-3��
��n��=2ʱ��x-1=2����x=3��
��-2��n���4��
����ͼ���֪��k��ȡֵ��Χ�ǣ�3��k��5��
��3�����ڣ��������£�
��y=-x2-4tx+4t2+3t=-��x+2t��2+8t2+3t���ඥ������Ϊ��-2t��8t2+3t����
ͼ���ϵĵ�P�ľ��Ե�Q���ں���n����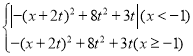 ��ͼ���ϣ�
��ͼ���ϣ�
����-2t��-1����ͼ2��
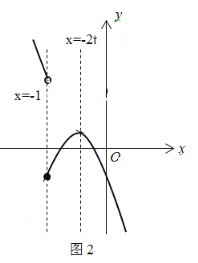
��x��-1ʱ��n�䣾|-��-1+2t��2+8t2+3t|=|4t2+7t-1|����a=-4t2-7t+1��
��x��-1ʱ��n���8t2+3t����b=8t2+3t��
��s=a-b=-12t2-10t+1=-12(t+![]() )2+
)2+![]() ��
��
�൱t=-![]() ʱ��sȡ�����ֵ
ʱ��sȡ�����ֵ![]() ��
��
����-2t��-1����ͼ3��
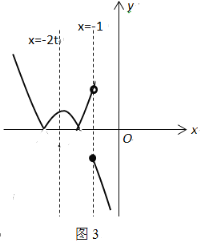
��x��-1ʱ��n���0����x��-1ʱ��n���4t2+7t-1��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��![]() ��������ȥ��
��������ȥ��
������������t=-![]() ʱ��sȡ�����ֵ
ʱ��sȡ�����ֵ![]() ��
��

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
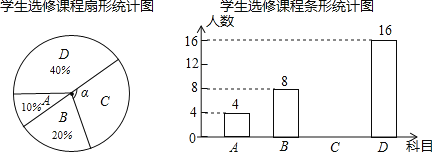
������������Ӧ����ϵ�д�����Ŀ�������ڼ䣬���г�![]() ����ʦ��Ϊ�˽⺢�����ڼ�ÿ������������������ռ��������ݲ������������в������IJ�����������ִ�����������ͳ��ͼ������ͳ��ͼ��
����ʦ��Ϊ�˽⺢�����ڼ�ÿ������������������ռ��������ݲ������������в������IJ�����������ִ�����������ͳ��ͼ������ͳ��ͼ��
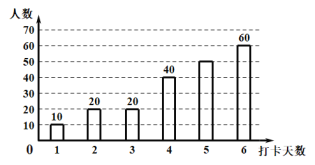
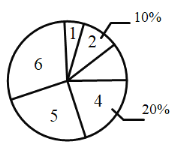
ͨ����������![]() ��ͳ��ͼ���������±���
��ͳ��ͼ���������±���
ͳ���� | ƽ���� | ��λ�� | ���� |
���� | 4.4 | a | b |
��1����գ�![]() _______��
_______��![]() _______������ȫ����ͳ��ͼ��
_______������ȫ����ͳ��ͼ��
��2����Ϊ�����ڼ䣬�ڼ����������������ޣ����Թ涨��ִ�����![]() �켴Ϊ�ϸ�
�켴Ϊ�ϸ�![]() ������ѧ��
������ѧ��![]() �ˣ�������Ƴ�
�ˣ�������Ƴ�![]() ��ѧ�������������ϸ��������
��ѧ�������������ϸ��������
��3����ͳ��ʱ©��![]() ��ѧ�����Ƚ����Ĵ�������ԭͳ�ƵĴ������ϲ���һ�������ݺ���ƽ���������ˣ���©��������ѧ����ִ����������Ƕ����죿
��ѧ�����Ƚ����Ĵ�������ԭͳ�ƵĴ������ϲ���һ�������ݺ���ƽ���������ˣ���©��������ѧ����ִ����������Ƕ����죿
����Ŀ���ܡ��¹ڡ������Ӱ�죬ij����������������![]() ��
��![]() �����ͺŵġ���д�塱�������ķᣮ��֪
�����ͺŵġ���д�塱�������ķᣮ��֪![]() �ͣ�
�ͣ�![]() ����д����ۡ��ۼۺ�ÿ�������������ʾ��
����д����ۡ��ۼۺ�ÿ�������������ʾ��
���ۣ�Ԫ/���� | �ۼۣ�Ԫ/���� | ��������/�գ� | |
|
|
|
|
|
|
|
|
�����г����飬�������̶�![]() ����д�彵�����ۣ�ͬʱ��
����д�彵�����ۣ�ͬʱ��![]() ����д������ۼۣ���ʱ����
����д������ۼۣ���ʱ����![]() ����д��ÿ����
����д��ÿ����![]() Ԫ�Ϳɶ���
Ԫ�Ϳɶ���![]() ����
����![]() ����д��ÿ���
����д��ÿ���![]() Ԫ������
Ԫ������![]() ����Ҫ����ÿ�������������䣬������
����Ҫ����ÿ�������������䣬������![]() ����д��ÿ�������
����д��ÿ�������![]() ����ÿ���ܻ���������Ϊ
����ÿ���ܻ���������Ϊ![]() Ԫ
Ԫ
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��д��
֮��ĺ�����ϵʽ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��Ҫʹÿ���������![]() Ԫ��ֱ��д��
Ԫ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���������̾���ÿ����һ��![]() ����д�壬�;�
����д�壬�;�![]() Ԫ��
Ԫ��![]() ���¹����顱Ӱ������Ѽ�ͥ����
���¹����顱Ӱ������Ѽ�ͥ����![]() ʱ��ÿ����������Ϊ
ʱ��ÿ����������Ϊ![]() Ԫ����
Ԫ����![]() ��ֵ��
��ֵ��