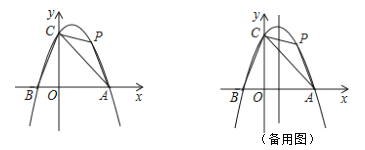题目内容
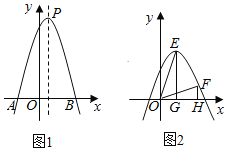
【题目】如图1,已知抛物线y=ax2+bx+c的顶点为P(1,9),与x轴的交点为A(﹣2,0),B.
(1)求抛物线的解析式;
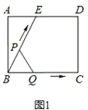
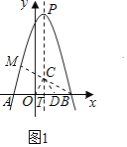
(2)M为x轴上方抛物线上的一点,MB与抛物线的对称轴交于点C,若∠COB=2∠CBO,求点M的坐标;
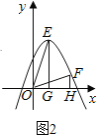
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为y=ax2+bx+h,E,F新抛物线在第一象限内互不重合的两点,EG⊥x轴,FH⊥x轴,垂足分别为G,H,若始终存在这样的点E,F,满足△GEO≌△HOF,求h的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设该抛物线解析式为![]() ,将点
,将点![]() 的坐标代入求得
的坐标代入求得![]() 的值即可;
的值即可;
(2)作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() ,结合三角形外角定理推知
,结合三角形外角定理推知![]() ,故
,故![]() .由勾股定理求得线段
.由勾股定理求得线段![]() 的长度,则
的长度,则![]() .由待定系数法确定直线
.由待定系数法确定直线![]() 解析式为
解析式为![]() ,与抛物线
,与抛物线![]() 联立得到:
联立得到:![]() .由此求得点
.由此求得点![]() 坐标;
坐标;
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,由全等三角形的对应边相等和二次函数图象上点的坐标特征建立
,由全等三角形的对应边相等和二次函数图象上点的坐标特征建立![]() 与
与![]() 或
或![]() 的函数关系式,从而求
的函数关系式,从而求![]() 的取值范围.
的取值范围.
解:(1)![]() 抛物线
抛物线![]() 的顶点为
的顶点为![]() ,
,
![]() 设该抛物线解析式为
设该抛物线解析式为![]() ,
,
把![]() 代入抛物线解析式得
代入抛物线解析式得![]() ,
,![]() ,
,
![]() ;
;
(2)令![]() 得
得![]() ,
,![]() ,或
,或![]() ,
,
![]() ,
,
![]()
抛物线对称轴直线![]() 与
与![]() 轴交点为
轴交点为![]() ,
,
如图1,作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,![]() .
.
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
与抛物线![]() 联立得
联立得![]() .
.
![]()
![]() ,
,![]() .
.
![]()
![]() ,
,
故点![]() 坐标为
坐标为![]() ;
;
(3)如图2,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设新抛物线解析式为![]() ,
,
把点![]() ,
,![]() 的坐标代入抛物线的解析式得:
的坐标代入抛物线的解析式得:![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 且
且![]()
把![]() 代入
代入![]() ,得
,得![]() .
.
![]() 且
且![]() .
.
![]()
![]() .
.
故![]() 的取值范围
的取值范围![]() .
.

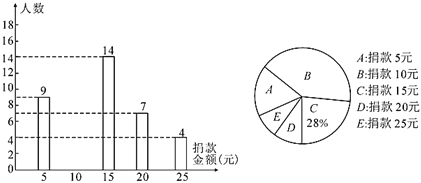
【题目】疫情期间,附中初![]() 级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
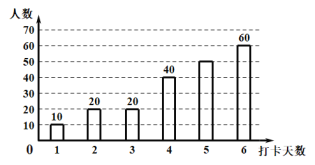
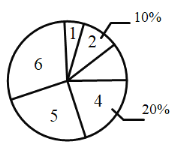
通过分析上面![]() 个统计图,制作如下表格:
个统计图,制作如下表格:
统计量 | 平均数 | 中位数 | 众数 |
天数 | 4.4 | a | b |
(1)填空:![]() _______,
_______,![]() _______,并补全条形统计图.
_______,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于![]() 天即为合格.初
天即为合格.初![]() 级共有学生
级共有学生![]() 人,请你估计初
人,请你估计初![]() 级学生中体育锻炼合格的人数.
级学生中体育锻炼合格的人数.
(3)若统计时漏掉![]() 名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?