Question

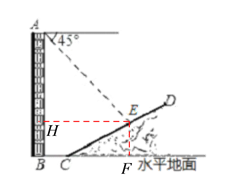
【题目】如图，一楼房AB后有一假山，山坡斜面CD与水平面夹角为30°，坡面上点E处有一亭子，测得假山坡脚C与楼房水平距离BC=10米，与亭子距离CE=20米，小丽从楼房顶测得点E的俯角为45°．求楼房AB的高（结果保留根号）．

Answer 1

【答案】楼房AB的高为（20+10）米．

【解析】试题分析：

如图，过点E作EF⊥BC于点F，作EH⊥AB于点H，先在Rt△CEF中已知条件解得：EF和CF的长，从而可得BF和HB的长，再由HE=BF可得HE的长；然后在Rt△AHE中由HE的长求得AH的长，最后由AB=AH+HB可得AB的长.

试题解析：

过点E作EF⊥BC于点F，EH⊥AB于点H．

∴∠EFC=∠EHA=∠EHB=∠HBC=90°.

∴四边形HBFE是矩形，

∴HE=BF，HB=EF，

∵在Rt△CEF中，CE=20，∠ECF=30°

∴EF=CE=10，CF=CEcos30°=，

∴HB=EF=10，BF=BC+CF=，

∴HE=BF=，

∵在Rt△AHE中，∠HAE=90°-45°=45°，

∴AH=HE=，

∴AB=AH+BH=10+10+10=20+10（米）

答：楼房AB的高为（20+10）米．