题目内容
【题目】在![]() 中,
中, ![]() ,点
,点![]() 是直线
是直线![]() 上一点(不与
上一点(不与![]() 重合),以
重合),以![]() 为一边在
为一边在![]() 的右侧作
的右侧作![]() ,使
,使![]() ,连接
,连接![]() .
.
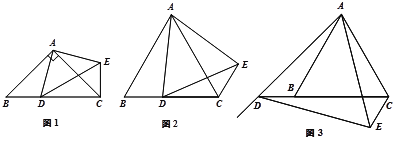
(1)如图1,当点![]() 在线段
在线段![]() 上,如果
上,如果![]() ,则
,则![]() 度;
度;
(2)设![]() ,
, ![]() .
.
①如图2,当点![]() 在线段
在线段![]() 上移动,则
上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点![]() 在直线
在直线![]() 上移动,则
上移动,则![]() 之间有怎样的数量关系?请画出图形并直接写出相应的结论.
之间有怎样的数量关系?请画出图形并直接写出相应的结论.

【答案】(1)90; (2) ①![]() .②
.②![]()
【解析】试题分析:(1)利用等腰三角形证明![]() ABD
ABD![]() ACE,所以∠ECA=∠DBA,所以∠DCE=90°.(2)方法类似(1)证明△ABD≌△ACE,所以∠B=∠ACE,再利用角的关系求
ACE,所以∠ECA=∠DBA,所以∠DCE=90°.(2)方法类似(1)证明△ABD≌△ACE,所以∠B=∠ACE,再利用角的关系求![]() . (3)同理方法类似(1).
. (3)同理方法类似(1).
试题解析:
解:(1) 90 度.
∠DAE=∠BAC ,所以∠BAD=∠EAC,AB=AC,AD=AE,所以![]() ABD
ABD![]() ACE,所以∠ECA=∠DBA,所以∠ECA=90°.
ACE,所以∠ECA=∠DBA,所以∠ECA=90°.
(2)①![]() .
.
理由:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
又AB=AC,AD=AE,
∴△ABD≌△ACE,
∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB,
∴![]() .∵
.∵![]() ,
,
∴![]() .
.
(3)图形正确可知 ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目