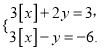题目内容
【题目】如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.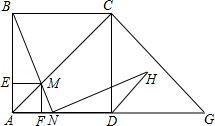
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.
【答案】
(1)
解:存在;当点M为AC的中点时,AM=BM,则△ABM为等腰三角形;
当点M与点C重合时,AB=BM,则△ABM为等腰三角形;
当点M在AC上,且AM=2时,AM=AB,则△ABM为等腰三角形;
当点M在AC上,且AM=BM时,AM= ![]() AC=
AC= ![]() ×2
×2 ![]() =
= ![]() 时,则△ABM为等腰三角形;
时,则△ABM为等腰三角形;
当点M为CG的中点时,AM=BM,则△ABM为等腰三角形;
(2)
证明:在AB上截取AK=AN,连接KN;如图1所示:

∵四边形ABCD是正方形,
∴∠ADC=90°,AB=AD,
∴∠CDG=90°,
∵BK=AB﹣AK,ND=AD﹣AN,
∴BK=DN,
∵DH平分∠CDG,
∴∠CDH=45°,
∴∠NDH=90°+45°=135°,
∴∠BKN=180°﹣∠AKN=135°,
∴∠BKN=∠NDH,
在Rt△ABN中,∠ABN+∠ANB=90°,
又∵BN⊥NH,
即∠BNH=90°,
∴∠ANB+∠DNH=180°﹣∠BNH=90°,
∴∠ABN=∠DNH,
在△BNK和△NHD中,
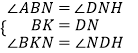 ,
,
∴△BNK≌△NHD(ASA),
∴BN=NH;
(3)
解:①当M在AC上时,即0<t≤2 ![]() 时,△AMF为等腰直角三角形,
时,△AMF为等腰直角三角形,
∵AM=t,
∴AF=FM= ![]() t,
t,
∴S= ![]() AFFM=
AFFM= ![]() ×
× ![]() t×
t× ![]() t=
t= ![]() t2;
t2;
当t=2 ![]() 时,S的最大值=
时,S的最大值= ![]() ×(2
×(2 ![]() )2=2;
)2=2;
②当M在CG上时,即2 ![]() <t<4
<t<4 ![]() 时,如图2所示:
时,如图2所示:
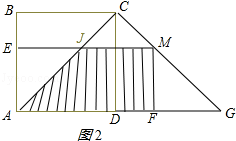
CM=t﹣AC=t﹣2 ![]() ,MG=4
,MG=4 ![]() ﹣t,
﹣t,
在△ACD和△GCD中,
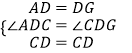 ,
,
∴△ACD≌△GCD(SAS),
∴∠ACD=∠GCD=45°,
∴∠ACM=∠ACD+∠GCD=90°,
∴∠G=90°﹣∠GCD=45°,
∴△MFG为等腰直角三角形,
∴FG=MGcos45°=(4 ![]() ﹣t)
﹣t) ![]() =4﹣
=4﹣ ![]() t,
t,
∴S=S△ACG﹣S△CMJ﹣S△FMG= ![]() ×4×2﹣
×4×2﹣ ![]() ×CM×CM﹣
×CM×CM﹣ ![]() ×FG×FG
×FG×FG
=4﹣ ![]() (t﹣2
(t﹣2 ![]() )2﹣
)2﹣ ![]() (4﹣
(4﹣ ![]() )2=﹣
)2=﹣ ![]() +4
+4 ![]() t﹣8
t﹣8
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,S的最大值为
时,S的最大值为 ![]() .
.
【解析】(1)四种情况:当点M为AC的中点时,AM=BM;当点M与点C重合时,AB=BM;当点M在AC上,且AM=2时,AM=AB;当点M在AC上,且AM=BM时,AM= ![]() 时;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;(3)①当M在AC上时,即0<t≤2
时;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;(3)①当M在AC上时,即0<t≤2 ![]() 时,△AMF为等腰直角三角形,得出AF=FM=
时,△AMF为等腰直角三角形,得出AF=FM= ![]() t,求出S=
t,求出S= ![]() AFFM=
AFFM= ![]() t2;当t=2
t2;当t=2 ![]() 时,即可求出S的最大值;
时,即可求出S的最大值;
②当M在CG上时,即2 ![]() <t<4
<t<4 ![]() 时,先证明△ACD≌△GD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MGcos45°=4﹣
时,先证明△ACD≌△GD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MGcos45°=4﹣ ![]() t,得出S=S△ACG﹣S△CMJ﹣S△FMG , S为t的二次函数,即可求出结果.
t,得出S=S△ACG﹣S△CMJ﹣S△FMG , S为t的二次函数,即可求出结果.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案【题目】为了推进我市校园体育运动的发展,2017年义乌市中小学运动会在雪峰中学成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:
篮球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 105 | 70 |
(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?