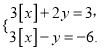Question

【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）=．

例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）=．

⑴如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．

求证：对任意一个完全平方数m，总有F（m）=1；

⑵如果一个两位正整数t，t ＝10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为54，那么我们称这个数t为“吉祥数”，求所有的“吉祥数”；

⑶在⑵所得“吉祥数”中，求 F（t）的最大值．

Answer 1

【答案】（1）见解析；（2）17，28，39；（3）

【解析】（1）对任意一个完全平方数m，设（为正整数），找出m的最佳分解，确定出的值即可；
（2）设交换t的个位上数与十位上的数得到的新数为t′，则，根据“吉祥数”的定义确定出x与y的关系式，进而求出所求即可；
（3）利用“吉祥数”的定义分别求出各自的值，进而确定出的最大值即可．

（1）对任意一个完全平方数m，设m=n2（n为正整数），
∵|n-n|=0，
∴n×n是m的最佳分解，
∴对任意一个完全平方数m，总有F（m）==1；
（2）设交换t的个位上的数与十位上的数得到的新数为t′，则
∵t为“吉祥数”，
∴
∴
∵ x，y为自然数，
∴“吉祥数”有：17，28，39，
（3）F（17）=，F（28）=，F（39）=，
∵＞＞，
∴所有“吉祥数”中，F（t）的最大值是．