ЬтФПФкШн
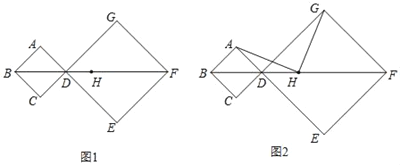
ЁОЬтФПЁПдке§ЗНаЮABCDКЭе§ЗНаЮDEFGжаЃЌЖЅЕуBЁЂDЁЂFдкЭЌвЛжБЯпЩЯЃЌHЪЧBFЕФжаЕуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєAB=1ЃЌDG=2ЃЌЧѓBHЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгAHЃЌGHЃЎ
аЁгюЙлВьЭМ2ЃЌЬсГіВТЯыЃКAH=GHЃЌAHЁЭGHЃЎаЁгюАбетИіВТЯыгыЭЌбЇУЧНјааНЛСїЃЌЭЈЙ§ЬжТлЃЌаЮГЩСЫжЄУїИУВТЯыЕФМИжжЯыЗЈЃК
ЯыЗЈ1ЃКбгГЄAHНЛEFгкЕуMЃЌСЌНгAGЃЌGMЃЌвЊжЄУїНсТлГЩСЂжЛашжЄЁїGAMЪЧЕШбќжБНЧШ§НЧаЮЃЛ
ЯыЗЈ2ЃКСЌНгACЃЌGEЗжБ№НЛBFгкЕуMЃЌNЃЌвЊжЄУїНсТлГЩСЂжЛашжЄЁїAMHЁеЁїHNGЃЎЁ
ЧыФуВЮПМЩЯУцЕФЯыЗЈЃЌАяжњаЁгюжЄУїAH=GHЃЌAHЁЭGHЃЎЃЈвЛжжЗНЗЈМДПЩЃЉ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉжЄУїМћНтЮі.
ЃЛЃЈ2ЃЉжЄУїМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнЙДЙЩЖЈРэЕУГіBDЃЌDFЃЌНјЖјЧѓГіBFЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯыЗЈ1ЁЂЯШХаЖЯЁїABHЁеЁїMFHЃЌНјЖјХаЖЯГіЁїADGЁеЁїMFGЃЎМДПЩХаЖЯГіЁїAGMЮЊЕШбќжБНЧШ§НЧаЮЃЌМДПЩЕУГіНсТлЃЛ
ЯыЗЈ2ЁЂЯШХаЖЯГіMN=![]() BFЃЎНјЖјХаЖЯГіЁїAMHЁеЁїHNGЃЌМДПЩХаЖЯГіЁЯAHM+ЁЯGHN=90ЁуЃЎМДПЩЕУГіНсТлЃЎ
BFЃЎНјЖјХаЖЯГіЁїAMHЁеЁїHNGЃЌМДПЩХаЖЯГіЁЯAHM+ЁЯGHN=90ЁуЃЎМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпе§ЗНаЮжаABCDКЭе§ЗНаЮDEFGЃЌЁрЁїABDЃЌЁїGDFЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЁпAB=1ЃЌDG=2ЃЌЁргЩЙДЙЩЖЈРэЕУBD=![]() ЃЌDF=2
ЃЌDF=2![]() ЃЎ
ЃЎ
ЁпBЁЂDЁЂFЙВЯпЃЌЁрBF=3![]() ЃЎ
ЃЎ
ЁпHЪЧBFЕФжаЕуЃЌЁрBH=![]() BF=
BF=![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЯыЗЈ1ЃК
ШчЭМ1ЃЌбгГЄAHНЛEFгкЕуMЃЌСЌНгAGЃЌGMЃЎ
Ёпе§ЗНаЮжаABCDКЭе§ЗНаЮDEFGЧвBЁЂDЁЂFЙВЯпЃЌЁрABЁЮEFЃЌЁрЁЯABH=ЁЯMFHЃЎ
гжЁпBH=FHЃЌЁЯAHB=ЁЯMHFЃЌЁрЁїABHЁеЁїMFHЃЌЁрAH=MHЃЌAB=MFЃЎ
ЁпAB=ADЃЌЁрAD=MFЃЎ
ЁпDG=FGЃЌЁЯADG=ЁЯMFG=90ЁуЃЌЁрЁїADGЁеЁїMFGЃЌЁрЁЯAGD=ЁЯMGFЃЌAG=MGЃЎ
гжЁпЁЯDGM+ЁЯMGF=90ЁуЃЌЁрЁЯAGD+ЁЯDGM=ЁЯAGM=90ЁуЃЌЁрЁїAGMЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЁпAH=MHЃЌЁрAH=GHЃЌAHЁЭGHЃЎ
ЯыЗЈ2ЃК
ШчЭМ2ЃЌСЌНгACЃЌGEЗжБ№НЛBFгкЕуMЃЌNЃЎ
Ёпе§ЗНаЮжаABCDКЭе§ЗНаЮDEFGЧвBЁЂDЁЂFЙВЯпЃЌЁрACЁЭBFЃЌGEЁЭBFЃЌDM=AM=![]() BDЃЌDN=GN=
BDЃЌDN=GN=![]() DFЃЌЁрЁЯAMD=ЁЯGNH=90ЁуЃЌMN=
DFЃЌЁрЁЯAMD=ЁЯGNH=90ЁуЃЌMN=![]() BFЃЎ
BFЃЎ
ЁпHЪЧBFЕФжаЕуЃЌЁрBH=![]() BFЃЌЁрBH=MNЃЌЁрBHЉMH=MNЉMHЃЌЁрBM=HNЃЎ
BFЃЌЁрBH=MNЃЌЁрBHЉMH=MNЉMHЃЌЁрBM=HNЃЎ
ЁпAM=BM=DMЃЌЁрAM=HN=DMЃЌЁрMD+DH=NH+DHЃЌЁрMH=DNЃЎ
ЁпDN=GNЃЌЁрMH=GNЃЎ
дкЁїAMHКЭЁїHNGжаЃЌЁпAM=HNЃЌЁЯAMD=ЁЯHNGЃЌMH=NGЃЌЁрЁїAMHЁеЁїHNGЃЌЁрAH=GHЃЌЁЯAHM=ЁЯHGNЃЎ
ЁпЁЯHGN+ЁЯGHN=90ЁуЃЌЁрЁЯAHM+ЁЯGHN=90ЁуЃЌЁрЁЯAHG=90ЁуЃЌЁрAHЁЭGHЃЌЁрAH=GHЃЌAHЁЭGHЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ