题目内容
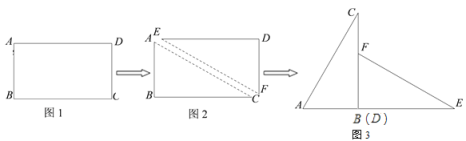
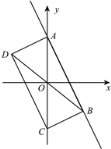
【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
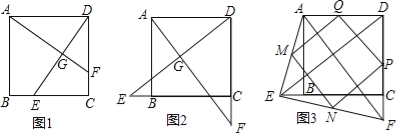
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
【答案】(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.
【解析】
试题(1)因为四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠DAF=∠CDE,又因为∠ADG+∠EDC=90°,即有AF⊥DE;
(2)∵四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠E=∠F,又因为∠ADG+∠EDC=90°,即有AF⊥DE;
(3)设MQ,DE分别交AF于点G,O,PQ交DE于点H,因为点M,N,P,Q分别为AE,EF,FD,AD的中点,可得MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,然后根据AF=DE,可得四边形MNPQ是菱形,又因为AF⊥DE即可证得四边形MNPQ是正方形.
AF,MQ∥DE,PQ∥AF,然后根据AF=DE,可得四边形MNPQ是菱形,又因为AF⊥DE即可证得四边形MNPQ是正方形.
试题解析:(1)上述结论①,②仍然成立,理由是:
∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠DAF=∠CDE,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;
(2)上述结论①,②仍然成立,理由是:
∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠E=∠F,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;
(3)四边形MNPQ是正方形.理由是:
如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,∵点M,N,P,Q分别为AE,EF,FD,AD的中点,
∴MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,∴四边形OHQG是平行四边形,∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形,∵AF⊥DE,∴∠AOD=90°,∴∠HQG=∠AOD=90°,∴四边形MNPQ是正方形.
AF,MQ∥DE,PQ∥AF,∴四边形OHQG是平行四边形,∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形,∵AF⊥DE,∴∠AOD=90°,∴∠HQG=∠AOD=90°,∴四边形MNPQ是正方形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案