题目内容
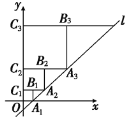
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1 , B2 , B3 , …,则B2017的坐标为( )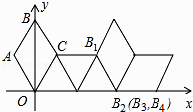
A.(1345,0)
B.(1345.5, ![]() )
)
C.(1345, ![]() )
)
D.(1345.5,0)
【答案】B
【解析】解:连接AC,
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.
画出第5次、第6次、第7次翻转后的图形.
由图可知:每翻转6次,图形向右平移4.
∵2017=336×6+1,
∴点B1向右平移1344(即336×4)到点B2017 .
∵B1的坐标为(1.5, ![]() ),
),
∴B2017的坐标为(1.5+1344, ![]() ),
),
∴B2017的坐标为(1345.5, ![]() ).
).
故答案为:(1345.5, ![]() ).
).
连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2017=336×6+1,因此点B1向右平移1344(即336×4)即可到达点B2017 , 根据点B5的坐标就可求出点B2017的坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目