题目内容
【题目】如图所示,CD是⊙O的弦,AB是⊙O的直径,且CD//AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E. 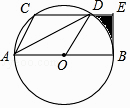
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分图形的周长(结果精确到1,参考数据:π=3.1, ![]() =1.4,
=1.4, ![]() =1.7).
=1.7).
【答案】
(1)证明:∵CD//AB,
∴∠CDA=∠DAO,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠CDA=∠ADO,
∴DA平分∠CDO
(2)解:∵AC=CD,
∴∠CDA=∠CAD,
∵∠CDA=∠ADO,
∴∠CAD=∠ADO,
∴AC//OD,
又∵AC=CD,CD//AB,
∴四边形AODC是菱形,
∴OA=AC,
连接OC,∵AB=12,
∴OA=AC=OC=6,
∴∠CAO=60°,
作CF⊥AB于点F,
∴CF=ACsin60°=6× ![]() =3
=3 ![]() ,AF=ACcos60°=3,
,AF=ACcos60°=3,
∵EB⊥AB,CD//AB,
则BE=CF=3 ![]() ,DE=AB﹣AF﹣CD=12﹣3﹣6=3,
,DE=AB﹣AF﹣CD=12﹣3﹣6=3,
∵∠CAO=60°,AC//DO,
∴∠CAO=∠DOB=60°,
∴ ![]() ,
,
∴图中阴影部分图形的周长是: ![]() =2π+3
=2π+3 ![]() +3=2×3.1+3×1.7+3≈14.
+3=2×3.1+3×1.7+3≈14.
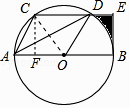
【解析】(1)要求DA平分∠CDO,只要求得∠CDA=∠ADO成立即可,根据题目中的条件,可以得到∠CDA=∠ADO,从而可以解答本题;(2)图中阴影部分图形的周长是BE+DE+ ![]() 的长,根据(1)中的结论和题目中的条件,可以求得BE+DE+
的长,根据(1)中的结论和题目中的条件,可以求得BE+DE+ ![]() 的长,从而可以解答本题.
的长,从而可以解答本题.
【考点精析】通过灵活运用切线的性质定理和弧长计算公式,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案