题目内容
【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
【答案】1+2+3+4+5;225;1+2+…+n;![]() ;11375
;11375
【解析】
观察题中的一系列等式发现,从1开始的连续正整数的立方和等于这几个连续正整数和的平方,根据此规律填空;(1)、根据上述规律填空,然后把1+2+…+n变为![]() 个(n+1)相乘,即可化简;(2)、对所求的式子前面加上1到10的立方和,然后根据上述规律分别求出1到15的立方和与1到10的立方和,求出的两数相减即可求出值.
个(n+1)相乘,即可化简;(2)、对所求的式子前面加上1到10的立方和,然后根据上述规律分别求出1到15的立方和与1到10的立方和,求出的两数相减即可求出值.
由题意可知:13+23+33+43+53=(1+2+3+4+5)2=225
(1)、∵1+2+…+n=(1+n)+[2+(n-1)]+…+[![]() +(n-
+(n-![]() +1)]=
+1)]=![]() ,
,
∴13+23+33+…+n3=(1+2+…+n)2=[![]() ]2;
]2;
(2)、113+123+133+143+153=13+23+33+…+153-(13+23+33+…+103)
=(1+2+…+15)2-(1+2+…+10)2 =1202-552=11375.

【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
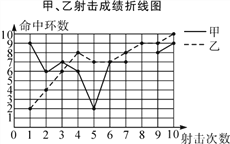
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?