Question

【题目】矩形ABCD中，AB＝8，AD＝6，P、Q是对角线BD上不重合的两点，点P关于直线AD，AB的对称点分别点E，F，点Q关于直线BC，CD的对称点分别是点G、H．若由点E，F，G，H构成的四边形恰好为菱形，则PQ的长为_____．

Answer 1

【答案】5.6

【解析】

根据轴对称求出AE=AF=AP，求出A、B、C、D都在菱形EFGH的边上，求出OA=AP=5，根据勾股定理求出ON，求出OP、OQ，即可得出答案．

矩形ABCD中，AB＝8，AD＝6，由勾股定理得：AC＝BD＝10，

如图，

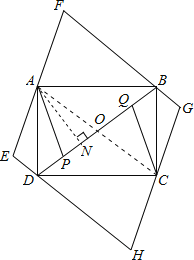
根据轴对称性质得：∠PAF+∠PAE＝90°+90°＝180°，

即A在菱形EFGH的边EF上，

同理B、C、D都在菱形EFGH的边上，

∵AP＝AF＝AE，即A为EF的中点，

同理C为GH的中点，

∵四边形EFGH是菱形，

∴AF＝CG，AF∥CG，

∴四边形AFGC是平行四边形，

∴FG＝AC＝10，

∵AE＝AF＝AP，

∴AP＝5，

∵AO＝AC＝5，

∴AO＝AP，

∴△APO是等腰三角形，

过A作AN⊥BD于N，

则N为OP的中点，

在Rt△DAB中，由三角形的面积公式得：AN×AB＝×AD×AB，

∴AN＝4.8，

由勾股定理得：ON＝＝1.4，

则OP＝2.8，

同理OQ＝2.8，

所以PQ＝2.8+2.8＝5.6，

故答案为：5.6