题目内容
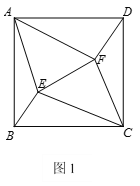
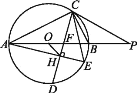
【题目】如图,△ABC内接于☉O,AB是☉O的直径,CD平分∠ACB交☉O于点D,交AB于点F,弦AE⊥CD于点H,连接CE、OH.
(1)延长AB到圆外一点P,连接PC,若PC2=PB·PA,求证:PC是☉O的切线;
(2)求证:CF·AE=AC·BC;
(3)若![]() =
=![]() ,☉O的半径是
,☉O的半径是![]() ,求tan∠AEC和OH的长.
,求tan∠AEC和OH的长.
【答案】(1)见解析;(2)见解析;(3) tan∠AEC=![]() ,OH =1.
,OH =1.
【解析】
(1)连接OC证明△PBC∽△PCA得∠BAC=∠PCB,可得∠PCO=90°,于是证得..
(2)△ACE、△CFB中,已知的相等角有∠CEA=∠CBA(同弧所对的圆周角),只需再找出一组对应角相等即可;易知∠ACB是直角,由于CD平分∠ACB,则∠ACH=∠FCB=45°;在Rt△CAH中,易证得∠HAC=45°,则∠CAH=∠FCB,由此得证;
(3)通过面积公式证明![]() =
=![]() .根据tan∠AEC=tan∠ABC=
.根据tan∠AEC=tan∠ABC=![]() 可求.AC=3k,BC=2k,在Rt△ACB中求出AC=6,BC=4.由△ACK是等腰直角三角形
可求.AC=3k,BC=2k,在Rt△ACB中求出AC=6,BC=4.由△ACK是等腰直角三角形
可得BK=6-4=2,又OH是△ABK的中位线,可得OH=![]() BK=1.
BK=1.
(1)证明:∵PC2=PB·PA,∴![]() =
=![]() ,
,
∵∠BPC=∠APC,∴△PBC∽△PCA,
∴∠BAC=∠PCB,连接OC,如图所示,
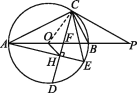
∵AO=OC,∴∠ACO=∠BAC,∴∠ACO=∠PCB.
∵AB是☉O的直径,∴∠ACB=90°,
∴∠BCO+∠ACO=90°,
∴∠BCO+∠PCB=90°,∴∠PCO=90°.
∵OC是半径,∴PC是☉O的切线.
(2)证明:∵AB是☉O的直径,∴∠ACB=90°.
∵CD平分∠ACB,∴∠ACD=∠FCB=45°.
∵AE⊥CD,∴∠CAE=45°=∠FCB.
在△ACE与△CFB中,
∠CAE=∠FCB,∠AEC=∠FBC,
∴△ACE∽△CFB,∴![]() =
=![]() ,
,
∴CF·AE=AC·BC.
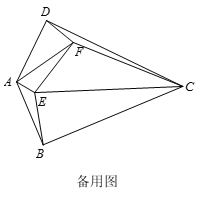
(3)作FM⊥AC于M,FN⊥BC于N,CQ⊥AB于Q,延长AE、CB交于点K.
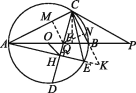
∵CD平分∠ACB,∴FM=FN.
∵S△ACF=![]() AC·FM=
AC·FM=![]() AF·CQ,
AF·CQ,
S△BCF=![]() BC·FN=
BC·FN=![]() BF·CQ,
BF·CQ,
∴![]() =
=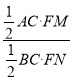 =
=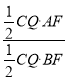 ,
,
∴![]() =
=![]() .
.
∵AB是☉O的直径,∴∠ACB=90°且tan∠ABC=![]() .
.
∵![]() =
=![]() 且∠AEC=∠ABC,
且∠AEC=∠ABC,
∴tan∠AEC=tan∠ABC=![]() =
=![]() .
.
设AC=3k,BC=2k,
∵在Rt△ACB中,AB2=AC2+BC2且AB=2![]() ,
,
∴(3k)2+(2k)2=(2![]() )2,∴k=2(k=-2舍去),
)2,∴k=2(k=-2舍去),
∴AC=6,BC=4,
∵∠FCB=45°,∠CHK=90°,
∴∠K=45°=∠CAE,
∴HA=HC=HK,CK=CA=6.
∵CB=4,∴BK=6-4=2,
∵OA=OB,HA=HK,
∴OH是△ABK的中位线,∴OH=![]() BK=1.
BK=1.

【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?