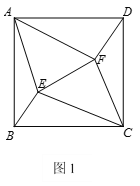
题目内容
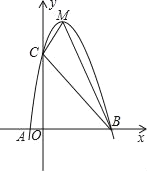
【题目】在四边形ABCD中，AB=AD，CB=CD，∠ABC=∠ADC=90°，∠BAD=α，∠BCD=β，点E，F是四边形ABCD内的两个点，满足∠EAF=
，∠ECF=
，连接BE，EF，FD．
（1）如图1，当α=β时，判断∠ABE和∠ADF之间的数量关系，并证明你的猜想；
（2）当α≠β时，用等式表示线段BE，EF，FD之间的数量关系(直接写出即可)
【答案】（1）∠ABE+∠ADF=90°，见解析；（2）BE2+DF2= EF2．
【解析】
（1）结论：∠ABE+∠ADF=90°．将△ABE绕点A逆时针旋转90°得到△ADM，将△BCE绕点C顺时针旋转90°得到△CDT，连接FM，TF．证明M，D，T共线，再证明FM=FT．DM=DT即可解决问题．
（2）结论：EF2=BE2+DF2．将△ABE绕点A逆时针旋转α度得到△ADM，将△BCE绕点C顺时针旋转β度得到△CDT，连接FM，TF．证明∠FDM=90°，利用勾股定理即可解决问题．
（1）结论：∠ABE+∠ADF=90°．
理由：∵AB=AD，CB=CD，∠ABC=∠ADC=90°，∠BAD=∠BCD，
∴∠BAD=∠BCD=90°，
∴四边形ABCD是正方形，
∴AB=BC=CD=AD，
将△ABE绕点A逆时针旋转90°得到△ADM，将△BCE绕点C顺时针旋转90°得到△CDT，连接FM，TF．
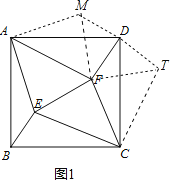
∵∠EAF=
×90°=45°，
∴∠MAD+∠DAF=∠BAE+∠DAF=45°，
∴∠FAM=∠FAE，
∵AM=AE，AF=AF，
∴△AFM≌△AFE（SAS），
∴EF=FM，
同法可证：EF=FT，
∴FM=FT，
∵∠ADM+∠CDT=∠ABE+∠CBE=90°，
∴∠MDT=90°+90°=180°，
∴M，D，T共线，
∵DM=BE，DT=BE，
∴DM=DT，
∴FD⊥MT，
∴∠FDM=90°，
∴∠ADM+∠ADF=90°，
∵∠ADM=∠ABE，
∴∠ABE+∠ADF=90°．
（2）结论：EF2=BE2+DF2．
理由：∵AD=AB，CD=CB，
∴将△ABE绕点A逆时针旋转α度得到△ADM，将△BCE绕点C顺时针旋转β度得到△CDT，连接FM，TF．
∵∠EAF=×∠DAB=α，
∴∠MAD+∠DAF=∠BAE+∠DAF=α，
∴∠FAM=∠FAE，
∵AM=AE，AF=AF，
∴△AFM≌△AFE（SAS），
∴EF=FM，
同法可证：EF=FT，
∴FM=FT，
∵∠ADM+∠CDT=∠ABE+∠CBE=90°，
∴∠MDT=90°+90°=180°，
∴M，D，T共线，
∵DM=BE，DT=BE，
∴DM=DT，
∴FD⊥MT，
∴∠FDM=90°，
∴FM2=DM2+DF2，
∵FM=EF，DM=BE，
∴EF2=BE2+DF2．
