题目内容
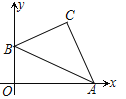
【题目】在平面直角坐标系中，已知点A、B的坐标分别为
A（6，0）、B（0，2），以AB为斜边在右上方作Rt△ABC.设点C坐标为（x，y），则（x+y）的最大值为__．
【答案】4+2
【解析】如图所示，
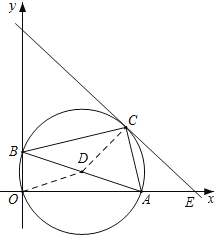
根据以AB为斜边在右上方作RtABC，可知点C在以AB为直径的⊙D上运动，根据点C坐标为（x，y）可构造新的函数x+y=m，则函数与y轴交点最高处即为x+y的最大值，此时，直线y=-x+m与⊙D相切，再根据圆心点的坐标，可得C的坐标，为（3+
，1+
），代入直线y=-x+m，可得4+2
，即可得出x+y的最大值为4+2
.
“点睛”本题主要考查了切线的性质，待定系数法求一次函数解析式以及等腰三角形的性质的综合应用，解决问题的关键是构造一次函数图象，根据圆的切线垂直于经过切点的半价进行求解.
练习册系列答案
寒假学与练系列答案
相关题目
