ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпyЃНЉ![]() x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпyЃН-
x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпyЃН-![]() x2+bx+cОЙ§BЁЂCСНЕуЃЌЕуPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPQЁЭxжсЃЌДЙзуЮЊQЃЌНЛжБЯпyЃНЉ
x2+bx+cОЙ§BЁЂCСНЕуЃЌЕуPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPQЁЭxжсЃЌДЙзуЮЊQЃЌНЛжБЯпyЃНЉ![]() x+2гкЕуDЃЎЩшЕуPЕФКсзјБъЮЊmЃЎ
x+2гкЕуDЃЎЩшЕуPЕФКсзјБъЮЊmЃЎ
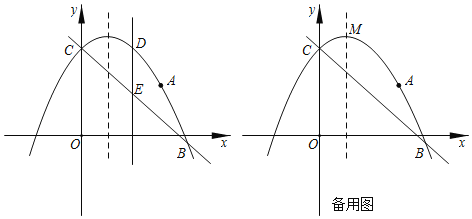
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєвдPЁЂDЁЂOЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓЕуQЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБЕуPЮЛгкжБЯпBCЩЯЗНЕФХзЮяЯпЩЯЪБЃЌЙ§ЕуPзїPEЁЭBCгкЕуEЃЌЧѓЕБPEШЁЕУзюДѓжЕЪБЕуPЕФзјБъЃЌВЂЧѓPEЕФзюДѓжЕЃЎ

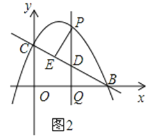
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2+
x2+![]() x+2ЃЛЃЈ2ЃЉ(2ЃЌ0)Лђ(2+2
x+2ЃЛЃЈ2ЃЉ(2ЃЌ0)Лђ(2+2![]() ЃЌ0)Лђ(2Љ2
ЃЌ0)Лђ(2Љ2![]() ЃЌ0)ЃЛЃЈ3ЃЉP(2ЃЌ3)ЃЌPEзюДѓжЕЮЊ
ЃЌ0)ЃЛЃЈ3ЃЉP(2ЃЌ3)ЃЌPEзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжБЯпyЃНЉ![]() x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCПЩЧѓГіBЁЂCСНЕузјБъЃЌДњШыyЃН-
x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCПЩЧѓГіBЁЂCСНЕузјБъЃЌДњШыyЃН-![]() x2+bx+cПЩЕУЙигкbЁЂcЕФЖўдЊвЛДЮЗНГЬзщЃЌНтЗНГЬзщЧѓГіbЁЂcЕФжЕМДПЩЕУД№АИЃЛ
x2+bx+cПЩЕУЙигкbЁЂcЕФЖўдЊвЛДЮЗНГЬзщЃЌНтЗНГЬзщЧѓГіbЁЂcЕФжЕМДПЩЕУД№АИЃЛ
ЃЈ2ЃЉИљОнPQЁЭxжсЃЌжБЯпyЃНЉ![]() x+2гкЕуDЃЌЕуPЕФКсзјБъЮЊmПЩгУmБэЪОГіDЁЂQСНЕузјБъЃЌИљОнЦНааЫФБпаЮЕФаджЪПЩЕУOC=PD=2ЃЌИљОнСНЕуМфОрРыЙЋЪНЧѓГіmЕФжЕМДПЩЕУД№АИЃЛ
x+2гкЕуDЃЌЕуPЕФКсзјБъЮЊmПЩгУmБэЪОГіDЁЂQСНЕузјБъЃЌИљОнЦНааЫФБпаЮЕФаджЪПЩЕУOC=PD=2ЃЌИљОнСНЕуМфОрРыЙЋЪНЧѓГіmЕФжЕМДПЩЕУД№АИЃЛ
ЃЈ3ЃЉРћгУЙДЙЩЖЈРэПЩЧѓГіBCЕФГЄЃЌИљОнЦНааЯпЕФаджЪПЩЕУЁЯOCBЃНЁЯPDEЃЌПЩжЄУїЁїPEDЁзЁїBOCЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪПЩгУmБэЪОГіPEЕФГЄЃЌИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЕУД№АИЃЎ
ЃЈ1ЃЉЁпжБЯпyЃНЉ![]() x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌ
x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌ
ЁрЕуBЁЂCЕФзјБъЗжБ№ЮЊЃЈ4ЃЌ0ЃЉЁЂЃЈ0ЃЌ2ЃЉЃЎ
ЁпХзЮяЯпyЃН-![]() x2+bx+cОЙ§BЁЂCСНЕуЃЌ
x2+bx+cОЙ§BЁЂCСНЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§БэДяЪНЮЊyЃНЉ![]() x2+
x2+![]() x+2ЃЎ
x+2ЃЎ
ЃЈ2ЃЉЁпPЕудкХзЮяЯпЩЯЃЌКсзјБъЮЊmЃЌ
ЁрPЕузјБъЮЊЃЈmЃЌЉ![]() m2+
m2+![]() m+2ЃЉЃЌ
m+2ЃЉЃЌ
ЁпPQЁЭxжсЃЌДЙзуЮЊQЃЌНЛжБЯпyЃНЉ![]() x+2гкЕуDЃЎ
x+2гкЕуDЃЎ
ЁрQзјБъЮЊЃЈmЃЌ0ЃЉЃЌDЕузјБъЮЊЃЈmЃЌЉ![]() m+2ЃЉЃЌ
m+2ЃЉЃЌ
ЕБPЁЂDЁЂOЁЂCЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЪБЃЌдђгаPDЃНOCЃН2ЃЌ
Ёр|Љ![]() m2+
m2+![]() m+2ЉЃЈЉ
m+2ЉЃЈЉ![]() m+2ЃЉ|ЃН2ЃЌМД|Љ
m+2ЃЉ|ЃН2ЃЌМД|Љ![]() m2+2m|ЃН2ЃЌ
m2+2m|ЃН2ЃЌ
ЕБЉ![]() m2+2mЃН2ЪБЃЌ
m2+2mЃН2ЪБЃЌ
НтЕУЃКmЃН2ЃЌ
ЁрQзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌ
ЕБЉ![]() m2+2mЃНЉ2ЪБЃЌ
m2+2mЃНЉ2ЪБЃЌ
НтЕУЃКmЃН2ЁР2![]() ЃЌ
ЃЌ
ЁрQзјБъЮЊЃЈ2+2![]() ЃЌ0ЃЉЛђЃЈ2Љ2
ЃЌ0ЃЉЛђЃЈ2Љ2![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
злЩЯПЩжЊЃКQЕузјБъЮЊЃЈ2ЃЌ0ЃЉЛђЃЈ2+2![]() ЃЌ0ЃЉЛђЃЈ2Љ2
ЃЌ0ЃЉЛђЃЈ2Љ2![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊPЕузјБъЮЊЃЈmЃЌЉ![]() m2+
m2+![]() m+2ЃЉЃЌQзјБъЮЊЃЈmЃЌ0ЃЉЃЌDЕузјБъЮЊЃЈmЃЌЉ
m+2ЃЉЃЌQзјБъЮЊЃЈmЃЌ0ЃЉЃЌDЕузјБъЮЊЃЈmЃЌЉ![]() m+2ЃЉЃЌ
m+2ЃЉЃЌ
ЁрPDЃНЉ![]() m2+2mЃЎ
m2+2mЃЎ
дкRtЁїOBCжаЃЌOCЃН2ЃЌOBЃН4ЃЌ
ЁрBCЃН![]() =2
=2![]() ЃЌ
ЃЌ
ЁпPQЁЮOCЃЌ
ЁрЁЯOCBЃНЁЯPDEЃЎ
ЁпPEЁЭBCЃЌ
ЁрЁЯPEDЃНЁЯCOBЃН90ЁуЃЎ
ЁрЁїPEDЁзЁїBOCЃЎ
Ёр![]() ЃЌ
ЃЌ
МД ЃЌ
ЃЌ
НтЕУPEЃН![]() ЃЌ
ЃЌ
ЁпPдкжБЯпBCЩЯЗНЃЌ
Ёр0ЃМmЃМ4ЃЌ
ЁрЕБmЃН2ЪБ PEгазюДѓжЕ![]() ЃЌ
ЃЌ
ЕБmЃН2ЪБЃЌЉ![]() m2+
m2+![]() m+2=3ЃЌ
m+2=3ЃЌ
ЁрДЫЪБPЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЎ

 ВНВНИпДяБъОэЯЕСаД№АИ
ВНВНИпДяБъОэЯЕСаД№АИ