题目内容
如图1,四边形ABCD是边长为2的菱形,且∠A=60°,将此菱形沿对角线裁剪,然后让△CBD沿着直线BD移动.(1)如图2,当△CBD移动到△CEF的位置时,连接BC、AF,求证:四边形ABCF是平行四边形.
(2)当△CBD向右移动距离为多少时,四边形ABCF为矩形;
(3)当△CBD向右平移4个单位时,求BC之间的距离.(画出图形)
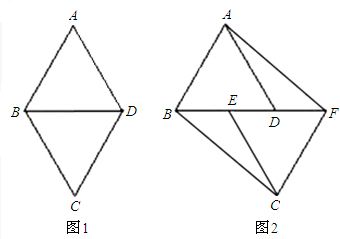
分析:(1)根据菱形的性质得出△ABD和△CEF是等边三角形且∠ABD=∠CFE=60°,即可得出四边形ABCF是平行四边形;
(2)根据对角线相等的平行四边形是矩形即可得出答案;
(3)过点C作CM⊥EF于点M,得出FM=1,CM=
,BM=5,再利用勾股定理求出.
(2)根据对角线相等的平行四边形是矩形即可得出答案;
(3)过点C作CM⊥EF于点M,得出FM=1,CM=
| 3 |
解答: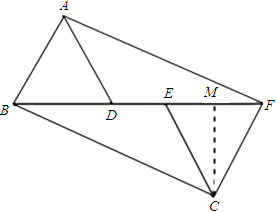 证明:(1)∵原四边形ABCD是菱形,∠BAD=60°,
证明:(1)∵原四边形ABCD是菱形,∠BAD=60°,
∴△ABD和△CEF是等边三角形且∠ABD=∠CFE=60°,
AB=CF,
∴AB∥CF.
∴四边形ABCF是平行四边形.
(2)根据(1)四边形ABCF是平行四边形.
∴E与D重合时,BF=AC=4,即可得出平行四边形是矩形,
∴当△CBD向右移动距离为2时,四边形ABCF为矩形;
(3)如图,过点C作CM⊥EF于点M
由题意可知,BF=6,CF=2,∠CFE=60°,
∴FM=1,CM=
,BM=5,
在Rt△BCM中,BC=
=
=2
.
 证明:(1)∵原四边形ABCD是菱形,∠BAD=60°,
证明:(1)∵原四边形ABCD是菱形,∠BAD=60°,∴△ABD和△CEF是等边三角形且∠ABD=∠CFE=60°,
AB=CF,
∴AB∥CF.
∴四边形ABCF是平行四边形.
(2)根据(1)四边形ABCF是平行四边形.
∴E与D重合时,BF=AC=4,即可得出平行四边形是矩形,
∴当△CBD向右移动距离为2时,四边形ABCF为矩形;
(3)如图,过点C作CM⊥EF于点M
由题意可知,BF=6,CF=2,∠CFE=60°,
∴FM=1,CM=
| 3 |
在Rt△BCM中,BC=
| 3+25 |
| 28 |
| 7 |
点评:此题主要考查了勾股定理以及平行四边形的判定方法以及矩形的判定方法和菱形的性质,熟练地区别矩形与菱形性质是解决问题的关键.

练习册系列答案
相关题目
 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.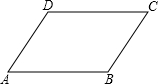 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.