题目内容
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂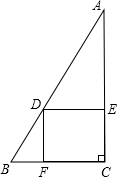 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y.(1)含y的代数式表示AE;
(2)y与x之间的函数关系式,并求出x的取值范围;
(3)设四边形DECF的面积为S,x在什么范围时s随x增大而增大.x在什么范围时s随x增大而减小,并画出s与x图象;
(4)求出x为何值时,面积s最大.
分析:(1)根据已知条件,结合矩形的性质,即可得出用y的代数式表示的AE;
(2)根据△DBF∽△ABC推出对应边的相似比,然后进行转换,即可得出y与x之间的函数关系式,随即结合图形可得x的取值范围;
(3)根据矩形的面积公式,很容易得出面积S关于x的二次函数表达式,根据表达式即可求出二次函数图象的顶点坐标、与x轴的交点,很容易即可画出图象;
(4)根据(3)中求出的二次函数表达式,求出顶点坐标,就可得出面积s最大时x的值.
(2)根据△DBF∽△ABC推出对应边的相似比,然后进行转换,即可得出y与x之间的函数关系式,随即结合图形可得x的取值范围;
(3)根据矩形的面积公式,很容易得出面积S关于x的二次函数表达式,根据表达式即可求出二次函数图象的顶点坐标、与x轴的交点,很容易即可画出图象;
(4)根据(3)中求出的二次函数表达式,求出顶点坐标,就可得出面积s最大时x的值.
解答:解:(1)∵在Rt△ABC中,∠C=90°,DE⊥AC,DF⊥BC,
∴四边形DECF为矩形,
∵DE=x,DF=y,
∴DF=EC=y,
∵AC=8,
∴AE=8-y;
(2)∵在Rt△ABC中,∠C=90°,DE⊥AC,DF⊥BC,BC=4,AC=8,
∴△DBF∽△ABC,
∴
=
,
∴
=
,
∴y=8-2x(0<x<4);
(3)∵矩形DECF,
∴S=xy=x(8-2x)=-2x2+8x;
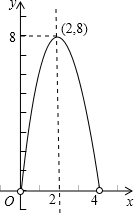
∴顶点坐标(2,8),与x轴的交点为(0,0),(4,0),
∴当0<x≤2时,S随x的增大而增大;
当2≤x<4时,S随x的增大而减小,
∴函数图象为
(4)∵由(3)的结论可知:x=-
=2,
∴当x=2时,面积S的值最大.
∴四边形DECF为矩形,
∵DE=x,DF=y,
∴DF=EC=y,
∵AC=8,
∴AE=8-y;
(2)∵在Rt△ABC中,∠C=90°,DE⊥AC,DF⊥BC,BC=4,AC=8,
∴△DBF∽△ABC,
∴
| DF |
| AC |
| BF |
| BC |
∴
| y |
| 8 |
| 4-x |
| 4 |
∴y=8-2x(0<x<4);

(3)∵矩形DECF,
∴S=xy=x(8-2x)=-2x2+8x;
∴顶点坐标(2,8),与x轴的交点为(0,0),(4,0),
∴当0<x≤2时,S随x的增大而增大;
当2≤x<4时,S随x的增大而减小,
∴函数图象为
(4)∵由(3)的结论可知:x=-
| b |
| 2a |
∴当x=2时,面积S的值最大.
点评:本题考查了相似三角形的判定及性质、二次函数的最值.关键在于根据相似三角形及已知条件求出相关线段的表达式,求出二次函数表达式,根据表达式画出图象后,即可求出结论.

练习册系列答案
相关题目
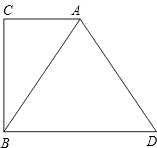 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.