题目内容
 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
分析:根据三角形中位线的定义以及性质定理、平行线分线段成比例定理进行证明.
解答: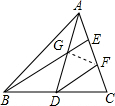 解:如右图所示,
解:如右图所示,
①∵AD是△ABC中线,
∴D是BC中点,
∵EF=FC,
∴F是CE中点,
∴DF是△CBE的中位线,
∴DF∥BE,
即DF∥GE,
故此选项正确;
②由①得DF∥GE,
又∵AE=EF,
∴AE:EF=AG:DG,
∴AG=DG,
∴EG是△ADF的中位线,
∴
DF=GE,
由①知DF是△CBE的中位线,
∴DF=
BE,
∴BG=
DF,
∴DF:BG=2:3,
此选项正确;
③由②知AG=DG,
此选项正确;
④连接GF,设BE、DF之间的距离是h,
根据题意,得
S△BDG=
BG•h,S四边形EFDG=S△DFG+S△EGF=
DF•h+
EG•h,
又∵DF:BG=2:3,
DF=GE,
∴S△BDG=
DF•h,S四边形EFDG=
DF•h,
∴S△BDG=S四边形EFDG,
此选项正确.
故选D.
 解:如右图所示,
解:如右图所示,①∵AD是△ABC中线,
∴D是BC中点,
∵EF=FC,
∴F是CE中点,
∴DF是△CBE的中位线,
∴DF∥BE,
即DF∥GE,
故此选项正确;
②由①得DF∥GE,
又∵AE=EF,
∴AE:EF=AG:DG,
∴AG=DG,
∴EG是△ADF的中位线,
∴
| 1 |
| 2 |
由①知DF是△CBE的中位线,
∴DF=
| 1 |
| 2 |
∴BG=
| 3 |
| 2 |
∴DF:BG=2:3,
此选项正确;
③由②知AG=DG,
此选项正确;
④连接GF,设BE、DF之间的距离是h,
根据题意,得
S△BDG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵DF:BG=2:3,
| 1 |
| 2 |
∴S△BDG=
| 3 |
| 4 |
| 3 |
| 4 |
∴S△BDG=S四边形EFDG,
此选项正确.
故选D.
点评:本题考查了三角形中位线定理、平行线分线段成比例定理.解题的关键是证明DF是△CBE的中位线,EG是△ADF的中位线.

练习册系列答案
相关题目

 如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是
如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是 16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为
16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为 如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.
如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )
如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )