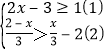��Ŀ����
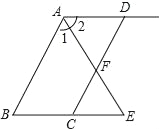
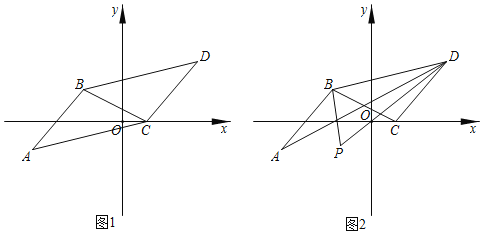
����Ŀ����ͼ����ͼ1����ƽ��ֱ������ϵ�У���֪��A����4����1����B����2��1�������߶�ABƽ�����߶�CD��ʹ��A�Ķ�Ӧ��C��x����������ϣ���D�ڵ�һ���ޣ�
��1������C�����꣨k��0�������D�����꣨�ú�k��ʽ�ӱ�ʾ����
��2������BD��BC����������BCD�����Ϊ5����k��ֵ��
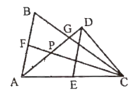
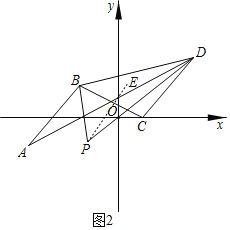
��3����ͼ2���ֱ�����ABC�͡�ADC��ƽ���ߣ����ǽ��ڵ�P����д����A���͡�P�͡�BCD֮���һ��������ϵ����˵�����ɣ�
���𰸡���1��D��k+2��2������2��k��2����3����BPD��![]() ��BCD+
��BCD+![]() ��A�������������
��A�������������
��������
��1����ƽ�Ƶ����ʿɵó��𰸣�
��2������B��BE��x���ڵ�E������D��DF��x���ڵ�F�����ı���BEFD������ɵó��𰸣�
��3������P��PE��AB�ó���PBA����EPB����ƽ�Ƶ����ʵó�AB��CD����ƽ���ߵ����ʵó�PE��CD�����EPD����PDC���ó���BPD����PBA+��PDC���ɽ�ƽ���ߵ����ʵó���PBA��![]() ��ABC����PDC��
��ABC����PDC��![]() ��ADC�����ɵó����ۣ�
��ADC�����ɵó����ۣ�
�⣺��1���ߵ�A����4����1����B����2��1����C��k��0�������߶�ABƽ�����߶�CD��
���B����ƽ��һ����λ������ƽ�ƣ�k+4������λ����D��
��D��k+2��2����
��2����ͼ1������B��BE��x���ڵ�E������D��DF��x���ڵ�F��
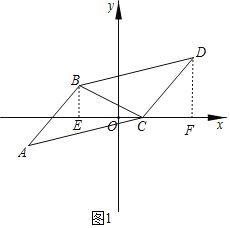
��A����4����1����B����2��1����C��k��0����D��k+2��2����
��BE��1��CE��k+2��DF��2��EF��k+4��CF��2��
��S�ı���BEFD��S��BEC+S��DCF+S��BCD��
��![]() ��
��![]() ��
��
��ã�k��2��
��3����BPD��![]() ��BCD+
��BCD+![]() ��A���������£�
��A���������£�
����P��PE��AB����ͼ2��ʾ��
���PBA����EPB��
���߶�ABƽ�����߶�CD��
��AB��CD��
��PE��CD����ADC����A����ABC����BCD��
���EPD����PDC��
���BPD����PBA+��PDC��
��BPƽ�֡�ABC��DPƽ�֡�ADC��
���PBA��![]() ��ABC����PDC��
��ABC����PDC��![]() ��ADC��
��ADC��
���BPD��![]() ��ABC+
��ABC+![]() ��ADC��
��ADC��![]() ��BCD+
��BCD+![]() ��A��
��A��

 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�����Ŀ��![]() ������һ����Ͷ�Ź������г�700�����������ó��У�����Ͷ������������ ���³�����Ҫ����ȴδ����������������ȡ��ij������ͬһʱ�εĵ������ݻ�����±���.
������һ����Ͷ�Ź������г�700�����������ó��У�����Ͷ������������ ���³�����Ҫ����ȴδ����������������ȡ��ij������ͬһʱ�εĵ������ݻ�����±���.
��ش���������:
ʱ�� | ��һ��7��00��8��00 | �ڶ���7��00��8��00 | ������7��00��8��00 | ������7��00��8��00 | ������7��00��8��00 |
��Ҫ�������г�ȴδ������������ˣ� | 1500 | 1200 | 1300 | 1300 | 1200 |
��1�������е�������ݣ�����������λ�������٣�
��2�����������������ƽ��ÿ����7:00-8:00 :��Ҫ���ù������г���������������