题目内容
【题目】如图①,△ABC是等边三角形,D、E分别为边BC和AC上的点,且BD=CE,过D作BE的平行线,过E作BC的平行线,它们交于点F,连接AF.
(1)求证:△ABE≌△CAD;
(2)试判断△ADF的形状,并说明理由;
(3)若将D、E分别移为边CB的延长线和AC的延长线上的点,其它条件不变(如图②),则△ADF的形状是否改变,说明理由.

【答案】(1)证明见解析(2)△ADF是等边三角形(3)△ADF仍是等边三角形
【解析】
(1)△ABE、△CAD中,已知的条件有:AB=AC,∠BAE=∠ACD=60°;若求两个三角形全等,只需再证得AE=CD即可,易知AC=BC,而BD=CE,即可得到AE=CD,由此得证;
(2)易证得四边形BDFE是平行四边形,则BE=DF=AD;设AD、BE交于G,则∠ADF=∠BGD;
而∠BGD=∠ABE+∠DAB,由(1)的全等三角形知:∠DAC=∠ABE,故∠BGD=∠DAC+∠DAB=60°,等量代换后,可求得∠ADF=60°,即可得到△ADF是等边三角形的结论.
(3)与(2)的结论相同,解题思路与(1)(2)完全相同.
(1)证明:∵△ABC是等边三角形,
∴∠BAE=∠C=60°,AB=AC=BC;
∵BD=CE,
∴AC﹣CE=BC﹣BD,∴AE=CD;
又AB=AC,
∴△ABE≌△CAD;
(2)△ADF是等边三角形,理由如下:
∵△ABC是等边三角形,∴∠BAC=60°;
∵DF∥BE,EF∥BC,
∴∠1=∠2,四边形BDFE是平行四边形;
∴BE=DF;
∵△ABE≌△CAD,∴∠4=∠5,BE=AD,∴DF=AD;
∵∠1=∠3+∠4,∴∠2=∠3+∠5=∠BAC=60°;
∴△ADF是等边三角形;
(3)△ADF仍是等边三角形,理由如下:
∵△ABC是等边三角形,∴∠ABC=∠BAE=∠C=60°,AB=BC;
∴∠ABD=∠BCD=180°﹣120°;
∵BD=CE,∴△ABD≌△BCE,∴∠1=∠3,BE=AD;
∵DF∥BE,EF∥BC,
∴∠1=∠2,四边形BDFE是平行四边形;
∴BE=DF,∴DF=AD;
∵∠3+∠4=∠ABC=60°,∴∠2+∠4=60°即∠ADF=60°
∴△ADF是等边三角形.

【题目】在我校“书香校园”活动中,某数学小组为了解学生家庭藏书情况,随机抽取我校部分学生进行调查,并绘制成部分统计图如下表:
类别 | 家庭藏书情况统计表 | 学生人数 |
|
| 20 |
|
|
|
|
| 50 |
|
| 66 |
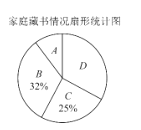
根据以上信息,解答下列问题:
(1)参加调查的学生人数为多少,a等于多少,本次调查结果的中位数在哪一类.
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为多少.
”对应扇形的圆心角为多少.
(3)若我校有4500名学生,请估计全校学生中藏书200本以上的人数.
【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别 | 阅读时间t(单位:小时) | 频数(人数) |
A | 0≤t<1 | 8 |
B | 1≤t<2 | 20 |
C | 2≤t<3 | 24 |
D | 3≤t<4 | m |
E | 4≤t<5 | 8 |
F | t≥5 | 4 |

(1)图表中的m= , n=;
(2)扇形统计图中F组所对应的圆心角为度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?