题目内容
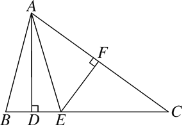
【题目】已知AB=5,AD=4,AD∥BM, ![]() (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,
(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x, ![]() .
.
(1)如图1,当x=4时,求AF的长;
(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】分析:作AH⊥BC于H,如图1,利用余弦的定义和勾股定理计算出BH=3,AH=4,AC=![]() ,再判断四边形ABCD为平行四边形得到∠B=∠D,接下来证明△ADF∽△ABC,然后利用相似比计算出AC;(2)如图2,先证明△BAC∽△BEA,利用相似比得到BE=
,再判断四边形ABCD为平行四边形得到∠B=∠D,接下来证明△ADF∽△ABC,然后利用相似比计算出AC;(2)如图2,先证明△BAC∽△BEA,利用相似比得到BE=![]() ,AC=
,AC= ![]() ,则CE=
,则CE= ![]() ,再证明△ADF∽EFC,利用相似比得到AF=
,再证明△ADF∽EFC,利用相似比得到AF= ![]() ,然后计算AF·AC可得到y与x的关系式,最后利用CE=
,然后计算AF·AC可得到y与x的关系式,最后利用CE= ![]() >0可确定x的范围;(3)讨论:当PA=PD时,作AH⊥BM于H,作PG⊥AD于G交BE于N,如图3,利用等腰三角形性质得AG=GD=2,BN=EN=
>0可确定x的范围;(3)讨论:当PA=PD时,作AH⊥BM于H,作PG⊥AD于G交BE于N,如图3,利用等腰三角形性质得AG=GD=2,BN=EN=![]() BE=
BE=![]() ,则
,则![]() =5,解方程易得x的值;当AP=AD=4时,先判断BP=EP=
=5,解方程易得x的值;当AP=AD=4时,先判断BP=EP=![]() ,则AE=4+
,则AE=4+![]() ,然后在RT△AHE中利用勾股定理得
,然后在RT△AHE中利用勾股定理得![]() ,则解方程可得到x的值;当DP=DA=4时,作AH⊥BM于H,作DK⊥BE于K,如图4,先确定BP=EB=
,则解方程可得到x的值;当DP=DA=4时,作AH⊥BM于H,作DK⊥BE于K,如图4,先确定BP=EB=![]() ,则BD=4+
,则BD=4+![]() ,再利用勾股定理计算出BD=
,再利用勾股定理计算出BD=![]() ,则4+
,则4+![]() =
=![]() ,然后解方程可得到x的值.
,然后解方程可得到x的值.
本题解析:(1)作A⊥BC于H如图,
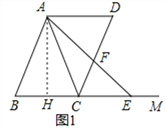
在RT△ABH中,∵cosB=![]() ,
,
∴BH=![]() ,∴CH=1,AH=
,∴CH=1,AH=![]() ,在RT△ACH中,AC=
,在RT△ACH中,AC=![]() ,
,
∵AD∥BC,AD=BC=4,∴四边形ABCD为平行四边形,∴∠B=∠D, ∵∠DAF=∠BAC, ∴△ADF∽△ABC, ∴![]() ,即
,即![]() ,∴AF=
,∴AF=![]() .
.
(2)如图,
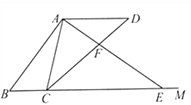
∵AD∥BE, ∴∠DAE=∠AEB,而∠DAE=∠BAC, ∴∠ABC=∠EBA, ∴△BAC∽△BEA, ∴![]() ,即
,即![]() ,∴BE=
,∴BE=![]() ,AC=
,AC= ![]() ,∴CE=BE-BC=
,∴CE=BE-BC=![]() -x, ∵AD∥CE, ∴△ADF∽△EFC, ∴
-x, ∵AD∥CE, ∴△ADF∽△EFC, ∴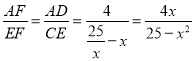 , ∴
, ∴![]() ,即AF=
,即AF= ![]() , ∴
, ∴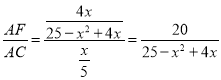 ,即y=
,即y=![]() ;
;
(3)当PA=PD时,作作AH⊥BM于H,作PG⊥AD于G交BE于N,如图,
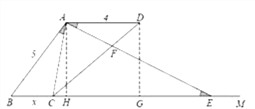
∵AD∥BE, ∴GN⊥BE, ∴AG=DG=2,BN=EN=![]() BE=
BE=![]() ,而BN=BH+CN=3+2=5,
,而BN=BH+CN=3+2=5,
∴![]() =5,解得x=
=5,解得x=![]() ;当AP=AD=4时,∵AD∥BE, ∴BP=EP=
;当AP=AD=4时,∵AD∥BE, ∴BP=EP=![]() ,
,
在Rt△AHE中, ![]() ,∴
,∴![]() ,解得x=
,解得x=![]() ;
;
当DP=DA=4时,作AH⊥BM于H,作DK⊥BE于K,如图4,∵AD∥BE, ∴BP=EP=![]() ,
,
∴BD=4+![]() ,在RT△BDK中,BD=
,在RT△BDK中,BD=![]() ,∴4+
,∴4+![]() =
=![]() ,∴x=
,∴x=![]() ,综上所述,x的值为
,综上所述,x的值为![]() 或
或![]() 或
或![]() .
.

 高中必刷题系列答案
高中必刷题系列答案【题目】蔬菜店店主老王,近两天经营的白菜和西兰花的情况如下:
(1)昨天的白菜和西兰花的进价和售价如下表,老王用![]() 元,批发白菜和西兰花共
元,批发白菜和西兰花共![]() 斤,当天售完后老王一共能赚多少元钱(请列方程解决问题)?
斤,当天售完后老王一共能赚多少元钱(请列方程解决问题)?
白菜 | 西兰花 | |
进价(元/斤) |
|
|
售价(元/斤) |
|
|
(2)今天因进价不变,老王仍用![]() 元批发白菜和西兰花共
元批发白菜和西兰花共![]() 斤.但在运输中白菜损坏了
斤.但在运输中白菜损坏了![]() ,而西兰花没有损坏且仍按昨天的售价销售,要想今天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给白菜定售价?(精确到
,而西兰花没有损坏且仍按昨天的售价销售,要想今天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给白菜定售价?(精确到![]() 元)
元)