题目内容
【题目】为了深入培养学生交通安全意识，加强实践活动，新华中学八年级（1）班和交警队联合举行了“我当一日小交警”活动，利用星期天到交通路口值勤，协助交通警察对行人、车辆及非机动车辆进行纠章．在这次实践活动中，若每一个路口安排5名学生，那么还剩下4人；若每个路口安排6人，那么最后一个路口不足3人，但不少于1人．
（1）求新华中学八年级（1）班有多少名学生？
（2）在值勤过程中，学生发现每辆汽车驶出路口后有三种方式前行：左转、直行、右转，而且每种前行方式的可能性相同．请通过画树形图或列表的方法，求连续驶出路口的两辆汽车前行路线相同的概率．
【答案】（1）新华中学八年级（1）班有44或49名学；（2）
【解析】
（1）设有x个交通路口，则八年级（1）班人数为（5x+4）名，根据题意列不等式组求解可得；
（2）由树状图求得所有等可能的结果与两辆汽车前行路线相同的情况，继而利用概率公式即可求得答案．
解：（1）设有x个交通路口，则八年级（1）班人数为（5x+4）名，
根据题意得
，
解得：7＜x≤9，
∵x为正整数，
∴x＝8或9，所以5x+4＝44或49．
答：新华中学八年级（1）班有44或49名学；
（2）列表可得：
第一辆 第二辆 | 左转 | 直行 | 右转 |
左转 | （左转，左转） | （直行，左转） | （右转，左转） |
直行 | （左转，直行） | （直行，直行） | （右转，直行） |
右转 | （左转，右转） | （直行，右转） | （右转，右转） |
由上表可知，所有可能发生的结果共有9种，并且它们发生的可能性都相等，
连续驶出路口的两辆汽车前行路线相同的有3种，分别为（左转，左转），（直行，直行），（右转，右转），
∴连续驶出路口的两辆汽车前行路线相同的概率为
，
答：连续驶出路口的两辆汽车前行路线相同的概率是．
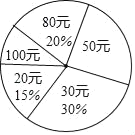
【题目】在“全民读书月”活动中，小明调查了班级里40名同学本学期购买课外书的费用情况，并将结果绘制成如图所示的统计表和扇形统计图，请根据相关信息，解答下列问题：(直接填写结果)
费用(元) | 20 | 30 | 50 | 80 | 100 |
人数 | 6 | a | 10 | b | 4 |
(1)本次调查获取的样本数据的众数是 元，中位数是 元；
(2)扇形统计图中，“50元”所对应的圆心角的度数为 度，该班学生购买课外书的平均费用为 元；
(3)若该校共有学生1000人，根据样本数据，估计本学期购买课外书花费50元的学生有 人．
