题目内容
【题目】已知P（﹣3，m）和 Q（1，m）是抛物线y=x2+bx﹣3上的两点．
（1）求b的值；
（2）将抛物线y=x2+bx﹣3的图象向上平移k（是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值；
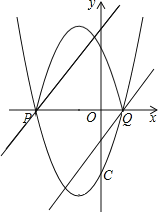
（3）将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线y=x+n与这个新图象有两个公共点时，求n的取值范围．
【答案】（1）2；（2）5；（3）n＞
或﹣1＜n＜3
【解析】
试题分析：（1）直接把点P，Q的坐标代入抛物线方程联立方程组求解b的值；
（2）利用图象与x轴无交点，则b2﹣4ac＜0，即可求出k的取值范围，进而得出k的值．
（3）求出两个边界点，继而可得出n的取值范围．
解：（1）∵P（﹣3，m）和 Q（1，m）是抛物线y=x2+bx﹣3上的两点，
∴
，解得：b=2；
（2）平移后抛物线的关系式为y=x2+2x﹣3+k．
要使平移后图象与x轴无交点，
则有b2﹣4ac=4﹣4（﹣3+k）＜0，
k＞4．
因为k是正整数，所以k的最小值为5．
（3）令x2+2x﹣3=0，
解之得：x1=1，x2=﹣3，
故P，Q两点的坐标分别为A（1，0），B（﹣3，0）．
如图，当直线y=x+n（n＜1），
经过P点时，可得n=3，
当直线y=x+n经过Q点时，
可得n=﹣1，
∴n的取值范围为﹣1＜n＜3，
翻折后的二次函数解析式为二次函数y=﹣x2﹣2x+3
当直线y=x+n与二次函数y=﹣x2﹣2x+3的图象只有一个交点时，
x+n=﹣x2﹣2x+3，
整理得：x2+3x+n﹣3=0，
△=b2﹣4ac=9﹣4（n﹣3）=21﹣4n=0，
解得：n=，
∴n的取值范围为：n＞，
由图可知，符合题意的n的取值范围为：n＞或﹣1＜n＜3．
