Question

【题目】在矩形ABCD中，AB=6，BC=12，点E在边BC上，且BE=2CE，将矩形沿过点E的直线折叠，点C，D的对应点分别为C′，D′，折痕与边AD交于点F，当点B，C′，D′恰好在同一直线上时，AF的长为_____．

Answer 1

【答案】8+或8﹣．

【解析】分析: 由折叠的性质得，∠EC′D′＝∠C＝90°，C′E＝CE，在Rt△BC′E中，由＝2，得到∠C′BE＝30°，①当点C′在BC的上方时，过E作EG⊥AD于G，延长EC′交AD于H，则四边形ABEG是矩形根据等边三角形的性质和矩形的性质，即可得到AF的长；②当点C′在BC的下方时，过F作FG⊥AD于G，D′F交BE于H，同①可得四边形ABGF是矩形根据矩形的性质和等边三角形的性质，即可得到AF的长．

详解: 由折叠的性质得，∠EC′D′＝∠C＝90°，C′E＝CE，

∵点B、C′、D′在同一直线上，

∴∠BC′E＝90°，

∵BC＝12，BE＝2CE，

∴BE＝8，C′E＝CE＝4，

在Rt△BC′E中，＝2，

∴∠C′BE＝30°，

①当点C′在BC的上方时，

如图1，过E作EG⊥AD于G，延长EC′交AD于H，则四边形ABEG是矩形，

∴EG＝AB＝6，AG＝BE＝8，

∵∠C′BE＝30°，∠BC′E＝90°，

∴∠BEC′＝60°，

由折叠的性质得，∠C′EF＝′CEF，

∴∠C′EF＝∠CEF＝60°，

∵AD∥BC

∴∠HFE＝∠CEF＝60°，

∴△EFH是等边三角形，

∴在Rt△EFG中，EG＝6，

∴GF＝2，

∴AF═8＋2；

②当点C′在BC的下方时，

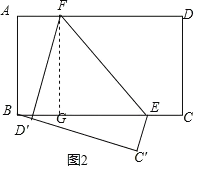
如图2，过F作FG⊥AD于G，D′F交BE于H，

同①可得，四边形ABGF是矩形，△EFH是等边三角形，

∴AF＝BG，FG＝AB＝6，∠FEH＝60°，

在Rt△EFG中，GE＝2，

∵BE＝8，

∴BG＝82，

∴AF＝82，

综上所述，AF的长是8＋2或82．

故答案为：8＋2或82．

点睛: 本题考查了翻折变换折叠问题，正确的作出图形是解题的关键．折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．