题目内容
【题目】如图,在△ABC中∠BAC=120°,AB=AC,点M、N在边BC上,且∠MAN=60°若BM=2,CN=3,则MN的长为_______.

【答案】![]()
【解析】
利用旋转作△APC,连接PN,根据旋转得:△ABM≌△ACP,PC=BM=2,证明△MAN≌△PAN,则MN=PN,作高线PD,利用勾股定理计算PD和PN的长,可得结论.
如图,△ABM绕点A逆时针旋转120°至△APC,连接PN,过点P作BC的垂线,垂足为D,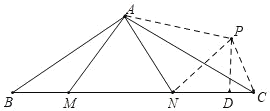
∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=30°,
由旋转可得△ABM≌△APC,
∴∠B=∠ACP=30°,PC=BM=2,∠BAM=∠CAP,
∴∠NCP=60°,
∵∠MAN=60°,
∴∠BAM+∠NAC=∠NAC+∠CAP=60°=∠MAN,
又∵AM=AP,AN=AN,
∴△MAN≌△PAN(SAS),
∴MN=PN,
∵PD⊥CN,∠NCP=60°
∴![]() ,
,![]()
∴DN=CN-CD=3-1=2,
∴![]()
∴MN=![]()

练习册系列答案
相关题目