题目内容
【题目】如图，AB∥CD，以点A为圆心，小于AC的长为半径画弧，分别交AB、AC于E、F两点；再分别以E、F为圆心，大于
的长为半径画弧，两弧交于点P，作射线AP，交CD于点M．若∠CMA＝25°，则∠C的度数为（ ）
A.100°B.110°C.120°D.130°
【答案】D
【解析】
连接PE、PF，根据SSS证△AFP≌△AEP，推出∠FAP=∠EAP，求出∠FAP=∠EAP=∠C=25°，根据三角形内角和定理求出即可．
解：连接PF、PE，
由作法可知：AF＝AE，PF＝PE，
∵在△AFP和△AEP中
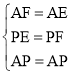
∴△AFP≌△AEP（SSS），
∴∠FAP＝∠EAP，
∵AB∥CD，
∴∠BAM＝∠CMA＝25°，
∴∠CAP＝25°，
∴∠C＝180°﹣∠CMA﹣∠CAP＝130°，
故选：D．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
