题目内容
【题目】探索与发现
探索：如图，在直角坐标系中，正方形ABCO的点B坐标（4，4），点A、C分别在y轴、x轴上，对角线AC上一动点E，连接BE，过E作DE⊥BE交OC于点D．
（1）证明：BE＝DE．
小明给出的思路为：过E作y轴的平行线交AB、x轴于点F、H．请完善小明的证明过程．
（2）若点D坐标为（3，0），则点E坐标为 ．
若点D坐标为（a，0），则点E坐标为 ．
发现：在直角坐标系中，点B坐标（5，3），点D坐标（3，0），找一点E，使得△BDE为等腰直角三角形，直接写出点E坐标．
【答案】（1）详见解析；（2）点D坐标为（1.5，2.5）；（0.5a，4﹣0.5a）；点E坐标为（0，2）或（2，5）或（6，﹣2）或（8，1）或（2.5，2.5）或（5.5，0.5）．
【解析】
（1）证出EH=BF，由ASA证明△BEF≌△EDH，得出BE=DE即可；
（2）连接OE，由正方形的对称性质得：OE=BE，证出OE=DE，由等腰三角形的性质得出OH=DH=
OD=1.5，由全等三角形的性质得出EF=DH=1.5，求出FH=OA=4，得出EH=2.5，得出点E的坐标为（1.5，2.5）；若点D坐标为（a，0），同理可得则点E坐标为（1.5a，2.5a）．
发现：分两种情况：
①当BD为等腰直角三角形的直角边长时，由全等三角形的性质和等腰直角三角形的性质得出点E的坐标为（0，2）或（2，5）或（6，-2）或（8，1）；
②当BD为等腰直角三角形的斜边长时，由全等三角形的性质和等腰直角三角形的性质点E的坐标为（2.5，2.5）或（5.5，0.5）；即可得出结论．
（1）证明：∵四边形ABCO是正方形，
∴AB∥OC，∠OAB＝∠AOC＝90°，∠OAC＝∠BAC＝∠OCA＝45°，OA∥BC，
∵FH∥AB，
∴FH∥OA，
∴FH⊥OC，∠HEC＝∠OAC＝45°＝∠OCA，∠BFH＝∠OAB＝90°，∠DHE＝∠AOC＝90°，
∴EH＝CH＝BF，
∵DE⊥BE，FH⊥AB，
∴由角的互余关系得：∠EBF＝∠DEH，
在△BEF和△EDH中，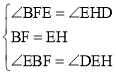
，
∴△BEF≌△EDH（ASA），
∴BE＝DE；
（2）解：连接OE，如图1所示：
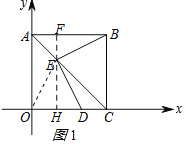
∵点D坐标为（3，0），
∴OD＝3，
由正方形的对称性质得：OE＝BE，
∵BE＝DE，
∴OE＝DE，
∵FH⊥OC，
∴OH＝DH＝OD＝1.5，
∵△BEF≌△EDH，
∴EF＝DH＝1.5，
∵FH＝OA＝4，
∴EH＝4﹣1.5＝2.5，
∴点E的坐标为（1.5，2.5）；
若点D坐标为（a，0），同理可得，点E坐标为（0.5a，4﹣0.5a）；
故答案为：（1.5，2.5）；（0.5a，4﹣0.5a）．
发现：分两种情况：
①当BD为等腰直角三角形的直角边长时，
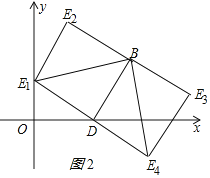
点E的坐标为（0，2）或（2，5）或（6，﹣2）或（8，1）；
②当BD为等腰直角三角形的斜边长时，
点E的坐标为（2.5，2.5）或（5.5，0.5）；
综上所述：△BDE为等腰直角三角形，点E坐标为（0，2）或（2，5）或（6，﹣2）或（8，1）或（2.5，2.5）或（5.5，0.5）．
