题目内容
【题目】如图，在半⊙O中，AB是直径，点D是⊙O上一点，点C是
的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE，CB于点P，Q，连接AC，关于下列结论：①∠BAD=∠ABC；②GP=GD；③点P是△ACQ的外心；④AC2=CQCB，其中结论正确的是____．
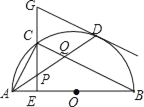
【答案】②③④
【解析】
点C是弧AD的中点，可得
，即可得∠BAD≠∠ABC，选项①错误；连接BD，由GD为圆O的切线，根据弦切角定理可得∠GDP=∠ABD，再由AB为圆的直径，根据直径所对的圆周角为直角得到∠ACB为直角，由CE⊥AB，得到∠AFP为直角，再由一对公共角，得到△APF与△ABD相似，根据相似三角形的对应角相等可得出∠APF=∠ABD，根据等量代换及对顶角相等可得出∠GPD=∠GDP，利用等角对等边可得出GP=GD，选项②正确；由直径AB⊥CE，利用垂径定理得到A为弧CE的中点，得到两条弧相等，再由C为弧AD的中点，得到两条弧相等，等量代换得到三条弧相等，根据等弧所对的圆周角相等可得出∠CAP=∠ACP，利用等角对等边可得出AP=CP，又AB为直径得到∠ACQ为直角，利用等角的余角相等可得出∠PCQ=∠PQC，得出CP=PQ，即P为直角三角形ACQ斜边上的中点，即为直角三角形ACQ的外心，选项③正确；利用等弧所对的圆周角相等得到一对角相等，再由一对公共角相等，得到△ACQ与△ABC相似，根据相似得比例得到AC2=CQCB，
∵在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，
∴弧AC=弧AD≠弧BD，
∴∠BAD≠∠ABC，选项①错误；
连接BD，如图所示：
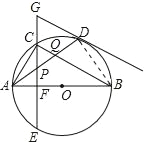
∵GD为圆O的切线，
∴∠GDP=∠ABD，
又AB为圆O的直径，∴∠ADB=90°，
∵CE⊥AB，∴∠AFP=90°，
∴∠ADB=∠AFP，又∠PAF=∠BAD，
∴△APF∽△ABD，
∴∠ABD=∠APF，又∠APF=∠GPD，
∴∠GDP=∠GPD，
∴GP=GD，选项②正确；
∵直径AB⊥CE，
∴A为弧CE的中点，即弧AE=弧AC，
又C为弧AD的中点，
∴弧AC=弧CD，
∴弧AE=弧CD，
∴∠CAP=∠ACP，
∴AP=CP，
又AB为圆O的直径，∴∠ACQ=90°，
∴∠PCQ=∠PQC，
∴PC=PQ，
∴AP=PQ，即P为Rt△ACQ斜边AQ的中点，
∴P为Rt△ACQ的外心，选项③正确；
连接CD，如图所示：
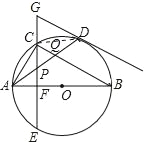
∵弧AC=弧CD，
∴∠B=∠CAD，
又∵∠ACQ=∠BCA，
∴△ACQ∽△BCA，
∴
，即AC2=CQCB，选项④正确，
综上可知则正确的选项序号有②③④，
故答案为：②③④．
