ΧβΡΩΡΎ»ί
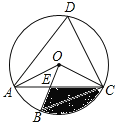
ΓΨΧβΡΩΓΩ ΐ―ßΩΈ…œΘ§άœ Π»Ο―ß…ζ≥ΏΙφΉςΆΦΜ≠RtΓςABCΘ§ ΙΤδ–±±ΏAB=cΘ§“ΜΧθ÷±Ϋ«±ΏBC=aΘ°άνΟςΒΡΉςΖ®»γΆΦΥυ ΨΘ§ΉςœΏΕΈAB ΙABΘΫCΘ§“‘ABΈΣ÷±ΨΕΉςΓ―OΘ§“‘BΈΣ‘≤–ΡΘ§aΈΣΑκΨΕΉςΜΓΫΜΓ―O”ΎΒψCΘ§Ν§Ϋ”ACΘ§ΓςABCΦ¥ΈΣΥυ«σΉςΒΡ»ΐΫ«–ΈΘ§Ρψ»œΈΣ’β÷÷ΉςΖ®÷–≈–ΕœΓœACB «÷±Ϋ«ΒΡ“άΨί «Θ®ΓΓΓΓΘ©
A. 90ΓψΒΡ‘≤÷ήΫ«ΥυΕ‘ΒΡœ“ «÷±ΨΕ B. ÷±ΨΕΥυΕ‘ΒΡ‘≤÷ήΫ« «÷±Ϋ«
C. Ι¥Ι…Ε®άμΒΡΡφΕ®άμ D. Ι¥Ι…Ε®άμ
ΓΨ¥πΑΗΓΩB
ΓΨΫβΈωΓΩ
ΗυΨίΉςΆΦΙΐ≥ΧΘ§ΫαΚœΓΑ‘Ύ‘≤÷–Θ§÷±ΨΕΥυΕ‘ΒΡ‘≤÷ήΫ« «÷±Ϋ«Γ±Ϋχ––Ζ÷Έω≈–ΕœΦ¥Ω….
”…ΉςΆΦΙΐ≥ΧΩ…÷ΣΘ§œΏΕΈAB «Γ―OΒΡ÷±ΨΕΘ§ΓœACB «Γ―O÷–ABΥυΕ‘ΒΡ‘≤÷ήΫ«Θ§
ΓύΓœACB=90ΓψΘ®÷±ΨΕΥυΕ‘ΒΡ‘≤÷ήΫ« «÷±Ϋ«Θ©Θ§
”÷ΓΏAB=cΘ§BC=aΘ§
ΓύΓςABCΈΣΥυ«σ»ΐΫ«–ΈΘ§«“ΓœACB «÷±Ϋ«.
Φ¥≈–ΕœΥυΉςΓςABC÷–ΓœACB «÷±Ϋ«ΒΡ“άΨί «ΘΚΓΑ÷±ΨΕΥυΕ‘ΒΡ‘≤÷ήΫ« «÷±Ϋ«Γ±.
Ι ―ΓB.

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΤΡœ Π¥σΗΫ–Γ“ΜœΏΟϊ ΠΧα”≈Ής“ΒœΒΝ–¥πΑΗ
‘ΤΡœ Π¥σΗΫ–Γ“ΜœΏΟϊ ΠΧα”≈Ής“ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ