Question

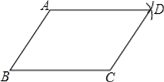
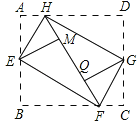
【题目】如图将矩形ABCD的四个内角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，EH=12，EF=16，则边AB的长是（　　）

A. 8+6B. 12C. 19.2D. 20

Answer 1

【答案】C

【解析】

先求出△EFH是直角三角形，再根据勾股定理求出FH=20，再利用三角形等面积法求出EM即可求出AB的长．

如图所示：设HF上两个点分别为M、Q，

∵M点是B点对折过去的，

∴∠EMH为直角，△AEH≌△MEH，

∴∠HEA＝∠MEH，

同理∠MEF＝∠BEF，

∴∠MEH＋∠MEF＝90°，

∴四边形EFGH是矩形，

∴△DHG≌△BFE，△HEF是直角三角形，

∴BF＝DH＝MF，

∵AH＝HM，∴AD＝HF，

∵EH＝12，EF＝16，

∴FH＝＝，

∴AE＝EM＝，

则BE=AE＝EM=9.6，

∴AB＝AE＋BE＝9.6＋9.6＝19.2．