题目内容
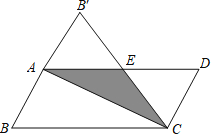
【题目】如图,在平行四边形纸片ABCD中,AB=3cm,将纸片沿对角线AC对折,BC边的对应边B′C与AD边交于点E,此时△CDE恰为等边三角形中,求:
(1)AD的长度.
(2)重叠部分的面积.
【答案】(1)AD=6cm;(2)S△ACE=![]() cm2.
cm2.
【解析】
(1)首先根据等边三角形的性质可得DF=DC=EC,∠D=60°,根据折叠的性质,∠BCA=∠B′CA,再利用平行四边形的性质证明∠DAC=30°,∠ACD=90°,利用直角三角形30°角所对的边等于斜边的一半可得CD长,进而可得AB的长;
(2)利用三角函数值计算出AC,然后根据三角形的中线平分三角形的面积可得S△ACE=![]() S△ACD,进而可得答案.
S△ACD,进而可得答案.
解:(1)∵△CDE为等边三角形,
∴DE=DC=EC,∠D=60°,
根据折叠的性质,∠BCA=∠B′CA,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6cm,AB=CD,
∴∠EAC=∠BCA,
∴∠EAC=∠ECA,
∴EA=EC,
∴∠DAC=30°,
∴∠ACD=90°,
∴AD=2CD=6cm;
(2)∵CD=3cm,∠ACD=90°,∠DAC=30°,
∴AC=3![]() cm,
cm,
∴S△ACE=![]() ×AC×
×AC×![]() CD=
CD=![]() cm2.
cm2.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目