题目内容
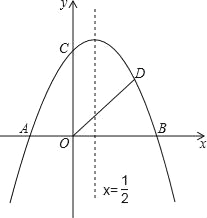
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=
x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=![]() ,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
(1)求抛物线的解析式和点D的坐标;
(2)点M是抛物线上的动点,在x轴上存在一点N,使得A、D、M、N四个点为顶点的四边形是平行四边形,求出点M的坐标;
(3)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3,(2,2);(2)(﹣1,2)或(
x+3,(2,2);(2)(﹣1,2)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2);(3)存在,(
,﹣2);(3)存在,( ![]() ,
, ![]() ).
).
【解析】(1)由于A、B关于抛物线的对称轴对称,根据对称轴方程求出B点的坐标,然后将它们代入抛物线的解析式可求出待定系数的值;OD平分∠BOC,那么直线OD的解析式为y=x,联立抛物线的解析式即可求出D点的坐标;
(2)分两种情况讨论:①以AD为对角线的平行四边形AMDN,此时MD∥x轴,则M、D的纵坐标相同,由此可求得M点的坐标;②以AD为边的平行四边形ADNM,由于平行四边形是中心对称图形,可求得△ADM≌△ADN,即M、N纵坐标的绝对值相等,可据此求出M点的坐标;
(3)由于BD的长为定值,若△BPD的周长最短,那么PB+PD应该最短,由于A、B关于抛物线的对称轴对称,连接AD,直线AD与对称轴的交点即为所求的P点,可用待定系数法求出直线AD的解析式,联立抛物线对称轴方程即可得到P点坐标.
解:(1)∵OA=2,
∴A(﹣2,0).
∵A与B关于直线x=![]() 对称,
对称,
∴B(3,0),
∵A、B,两点在抛物线y=﹣![]() x2+bx+c上,
x2+bx+c上,
∴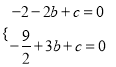 ,
,
解得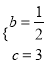 ;
;
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+3.
x+3.
过D作DE⊥x轴于E.
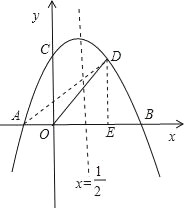
∵∠BOC=90°,OD平分∠BOC,
∴∠DOB=45°,∠ODE=45°,
∴DE=OE,即xD=yD,
∴x=﹣![]() x2+
x2+![]() x+3,
x+3,
解得x1=2,x2=﹣3(舍去),
∴D(2,2);
(2)分两种情况讨论:
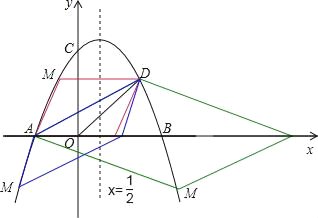
①当AD为平行四边形AMDN的对角线时,
∵MD∥AN,即MD∥x轴,
∴yM=yD,
∴M与D关于直线x=![]() 对称,
对称,
∴M(﹣1,2);
②当AD为平行四边形ADNM的边时,
∵平行四边形ADNM是中心对称图形,△AND≌△ANM,
∴|yM|=|yD|,即yM=﹣yD=﹣2,
∴令﹣![]() x2+
x2+![]() x+3=﹣2,即x2﹣x﹣10=0;
x+3=﹣2,即x2﹣x﹣10=0;
解得x=![]() ,
,
∴M(![]() ,﹣2)或M(
,﹣2)或M(![]() ,﹣2).
,﹣2).
综上所述:满足条件的M点有3个,即M(﹣1,2)或M(![]() ,﹣2)或M(
,﹣2)或M(![]() ,﹣2);
,﹣2);
(3)∵BD为定值,
∴要使△BPD的周长最小,只需PD+PB最小.
∵A与B关于直线x=![]() 对称,
对称,
∴PB=PA,只需PD+PA最小.
连接AD,交对称轴于点P,此时PD+PA最小.
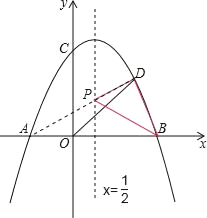
由A(﹣2,0),D(2,2)可得直线AD:y=![]() x+1,
x+1,
令x=![]() ,得y=
,得y=![]() ,
,
∴存在点P(![]() ,
, ![]() ),使△BPD的周长最小.
),使△BPD的周长最小.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为县级先进班集体,下表是三个班的五项素质考评得分表。
五项素质考评得分表(单位:分)
班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
甲班 | 10 | 10 | 6 | 10 | 7 |
乙班 | 10 | 8 | 8 | 9 | 8 |
丙班 | 9 | 10 | 9 | 6 | 9 |
根据统计表中的信息回答下列问题:
(1)请你补全五项成绩考评分析表中的数据:
班级 | 平均分 | 众数 | 中位数 |
甲班 | 8.6 | 10 | ③ |
乙班 | 8.6 | ② | 8 |
丙班 | ① | 9 | 9 |
(2)参照上表中的数据,你推荐哪个班为县级先进班集体?并说明理由。
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3∶2∶1∶1∶3的比确定班级的综合成绩,学生处的李老师根据这个综合成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,按照这个成绩,应推荐哪个班为县级先进班集体?为什么?