题目内容
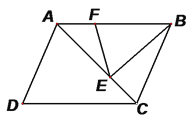
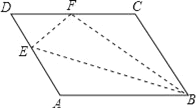
【题目】如图所示,在平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为7,△FCB的周长为19,求FC的长.
【答案】6
【解析】
由折叠的性质可得EF=AE,BF=AB,由四边形ABCD是平行四边形可得AD=BC,AB=DC,结合△FCB的周长=DF+DE+EF=DF+DE+AE=DF+AD=7和△FCB的周长=FC+BC+BF=FC+BC+AB=19可得平行四边形ABCD的周长=26,由此可得AD+DC=13,这样即可由FC=(AD+DC)-(AD+DF)求出FC的长.
∵△BEF是由△BDA沿BE折叠得到的,
∴EF=AE,BF=AB.
∵平行四边形ABCD,
∴AD=BC,AB=DC.
∵△FDE的周长=DF+DE+EF=7,
∴DF+DE+AE=7,即DF+AD=7.
∵△FCB的周长=FC+BC+BF=19,
∴FC+BC+AB=19,
∴平行四边形ABCD的周长=AD+DF+FC+BC+AB=7+19=26,
∴AD+DC=13,
∴FC=(AD+DC)-(AD+DF)=13-7=6.

练习册系列答案
相关题目
【题目】阅读下面材料:在数学课上,老师提出如下问题:
尺规作图,过圆外一点作圆的切线. |
小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A; |
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .