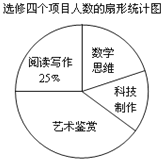
题目内容
【题目】阅读下面材料:在数学课上,老师提出如下问题:
尺规作图,过圆外一点作圆的切线. |
小涵的主要作法如下:
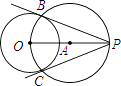
如图,(1)连结OP,作线段OP的中点A; |
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .
【答案】直径所对的圆周角是直角
【解析】解:∵OP是⊙A的直径,
∴∠PBO=∠PCO=90°,
∴OB⊥PB,OC⊥PC,
∵OB、OC是⊙O的半径,
∴PB、PC是⊙O的切线;
则小涵的作图依据是:直径所对的圆周角是直角.
故答案为:直径所对的圆周角是直角.
根据圆周角定理得出∠PBO=∠PCO=90°,即OB⊥PB,OC⊥PC,即可证得PB、PC是⊙O的切线.

练习册系列答案
相关题目
【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为![]() 元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) |
|
|
|
|
|
问
![]() 本周星期三黄金的收盘价是多少?
本周星期三黄金的收盘价是多少?
![]() 本周黄金收盘时的最高价、最低价分别是多少?
本周黄金收盘时的最高价、最低价分别是多少?
![]() 上周,小王以周五的收盘价
上周,小王以周五的收盘价![]() 元/克买入黄金
元/克买入黄金![]() 克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金
克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金![]() 克,他的收益情况如何?
克,他的收益情况如何?