题目内容
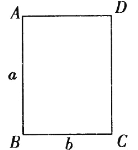
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是BC上的点.求证:BD2+CD2=2AD2 . 
【答案】证明:作AE⊥BC于E,如上图所示:
由题意得:ED=BD﹣BE=CE﹣CD,
∵在△ABC中,∠BAC=90°,AB=AC,
∴BE=CE= ![]() BC,
BC,
由勾股定理可得:
AB2+AC2=BC2 ,
AE2=AB2﹣BE2=AC2﹣CE2 ,
AD2=AE2+ED2 ,
∴2AD2=2AE2+2ED2=AB2﹣BE2+(BD﹣BE)2+AC2﹣CE2+(CE﹣CD)2
=AB2+AC2+BD2+CD2﹣2BD×BE﹣2CD×CE
=AB2+AC2+BD2+CD2﹣2× ![]() BC×BC
BC×BC
=BD2+CD2 ,
即:BD2+CD2=2AD2
【解析】作AE⊥BC于E,由于∠BAC=90°,AB=AC,所以BE=CE,要证明BD2+CD2=2AD2 , 只需找出BD、CD、AD三者之间的关系即可,由勾股定理可得出AD2=AE2+ED2 , AE2=AB2﹣BE2=AC2﹣CE2 , ED=BD﹣BE=CE﹣CD,代入求出三者之间的关系即可得证.

练习册系列答案
相关题目
【题目】我县某商场计划购进甲、乙两种商品共80件,这两种商品的进价、售价如表所示:
进价(元/件) | 售价(元/件) | |
甲种商品 | 15 | 20 |
乙种商品 | 25 | 35 |
设其中甲种商品购进x件,售完此两种商品总利润为y元.
(1)写出y与x的函数关系式.
(2)该商场计划最多投入1500元用于购进这两种商品共80件,则至少要购进多少件甲种商品?若售完这些商品,商场可获得的最大利润是多少元?