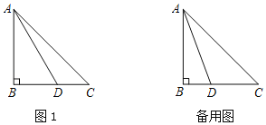��Ŀ����
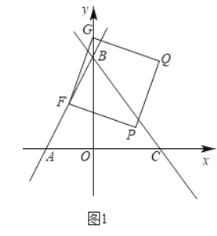
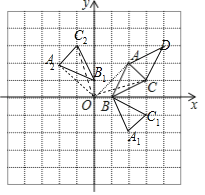
����Ŀ����ͼ����ABC�Ķ��������ֱ�ΪA��2��2����B��1��0����C��3��1����
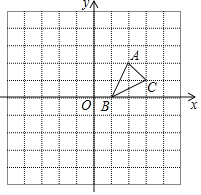
��1��������ABC����x��ԳƵ���A1BC1��д����C1������Ϊ�� ����
��2��������ABC��ԭ��O��ʱ����ת90������A2B1C2��д����C2������Ϊ�� ����
��3���ڣ�1������2���Ļ����ϣ�ͼ�е���A1BC1����A2B1C2���ڵ��� �����ĶԳƣ�
��4�����Ե�D��A��C��BΪ������ı���Ϊ���Σ�ֱ��д����D������Ϊ�� ����
���𰸡���1����3����1������2������1��3������3����![]() ��
��![]() ������4����4��4����
������4����4��4����
��������
��1�����ù���x�����������д��A1��C1�����꣬Ȼ����㼴�ɣ���2�����������ص����ת�����ʣ�д����A��B��C�Ķ�Ӧ��![]() ��
��![]() ��
��![]() ���Ӷ��õ���A2��B1��C2��Ȼ��д����C2�����ꣻ��3��д��B B1��A2 C1�Ľ������꼴�ɣ���4���Ȼ�������ABCD��Ȼ��д��D�����꣮
���Ӷ��õ���A2��B1��C2��Ȼ��д����C2�����ꣻ��3��д��B B1��A2 C1�Ľ������꼴�ɣ���4���Ȼ�������ABCD��Ȼ��д��D�����꣮
�⣺
��1����ͼ����A1B1C1Ϊ��������C1������Ϊ��3����1����
��2����ͼ����A2B2CΪ��������C2������Ϊ����1��3����
��3����A1BC1����A2B1C2���ڵ�![]() ���ĶԳƣ�
���ĶԳƣ�
��4����D��������4��4����
�ʴ�Ϊ��3����1��������1��3����![]() ����4��4����
����4��4����

 �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�����Ŀ��ij�̳���Ӫij��Ʒ�Ƶļ�����������ʱ�ĵ�����20Ԫ�������г����飺��һ��ʱ���ڣ����۵�����30Ԫʱ����������600���������۵���ÿ����1Ԫ���ͻ����۳�10����
��1�����������Ʒ�Ƽ����������۵���ΪxԪ��x��30��������ֱ���x�Ĵ���ʽ����ʾ������y�������۸�Ʒ�Ƽ������������wԪ�����ѽ����д�ڱ����У�
���۵��ۣ�Ԫ�� | x��x��30�� |
������y������ | �� �� |
���ۼ������������w��Ԫ�� | �� �� |
��2���ڵ���1���ʵ������£������������涨��Ʒ�Ƽ��������۵��۲�����35Ԫ�����̳�Ҫ��ɲ�����500���������������̳����۸�Ʒ�Ƽ����������������Ƕ��٣�