Question

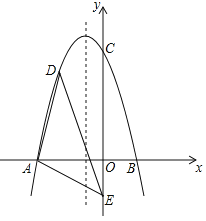
【题目】如图，顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1，0)，B两点，与y轴交于点C，过点C作CD⊥y轴交抛物线于另一点D，作DE⊥x轴，垂足为点E，双曲线y=(x＞0)经过点D，连接MD，BD．

（1）求抛物线的表达式；

（2）点N，F分别是x轴，y轴上的两点，当以M，D，N，F为顶点的四边形周长最小时，求出点N，F的坐标；

（3）动点P从点O出发，以每秒1个单位长度的速度沿OC方向运动，运动时间为t秒，当t为何值时，∠BPD的度数最大？

Answer 1

【答案】（1）y=﹣x2+2x+3；（2）N(，0)，F(0，)；（3）t=9﹣2．

【解析】

（1）由已知求出D点坐标，将点A（-1，0）和D（2，3）代入y=ax2+bx+3即可；

（2）作M关于y轴的对称点M'，作D关于x轴的对称点D'，连接M'D'与x轴、y轴分别交于点N、F，则以M，D，N，F为顶点的四边形周长最小即为M'D'+MD的长；

（3）设P（0，t），作△PBD的外接圆N，当⊙N与y轴相切时，∠BPD的度数最大；

解；（1）C(0，3)

∵CD⊥y，

∴D点纵坐标是3．

∵D在y=上，

∴D(2，3)，

将点A(﹣1，0)和D(2，3)代入y=ax2+bx+3，

∴a=﹣1，b=2，

∴y=﹣x2+2x+3；

（2）M(1，4)，B(3，0)，

作M关于y轴的对称点M'，作D关于x轴的对称点D'，连接M'D'与x轴、y轴分别交于点N、F，

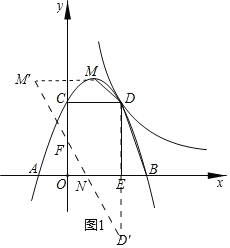
则以M，D，N，F为顶点的四边形周长最小即为M'D'+MD的长；

∴M'(﹣1，4)，D'(2，﹣3)，

∴M'D'直线的解析式为y=﹣x+，

∴N(，0)，F(0，)；

（3）设P(0，t)．

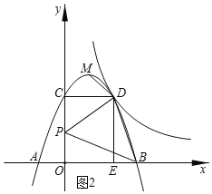
∵△PBO和△CDP都是直角三角形，

tan∠CDP=，tan∠PBO=，

令y=tan∠BPD=，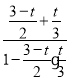

∴yt2+t﹣3yt+6y﹣9=0，

△=﹣15y2+30y+1=0时，

y=(舍)或y=，

∴t=﹣×，

∴t=9﹣2，

∴P(0，9﹣2)．