题目内容
【题目】
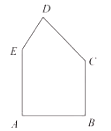
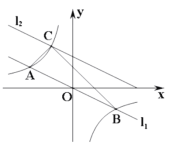
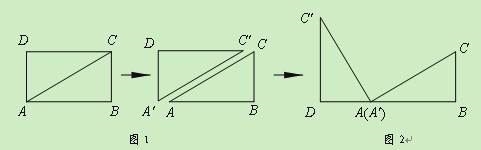
情境观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 ▲ ,∠CAC′= ▲ °.
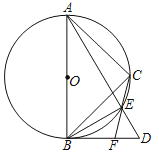
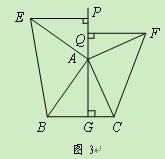
问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
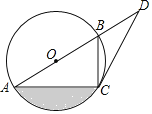
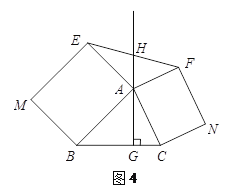
拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k AE,AC=k AF,试探究HE与HF之间的数量关系,并说明理由.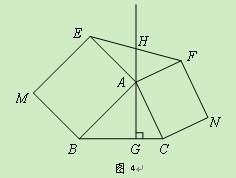
【答案】情境观察:AD(或A′D),90
问题探究:EP=FQ. 证明见解析
结论: HE=HF. 证明见解析
【解析】
情境观察
AD(或A′D),90
问题探究
结论:EP=FQ.
证明:∵△ABE是等腰三角形,∴AB=AE,∠BAE=90°.
∴∠BAG+∠EAP=90°.∵AG⊥BC,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.
∵EP⊥AG,∴∠AGB=∠EPA=90°,∴Rt△ABG≌Rt△EAP. ∴AG=EP.
同理AG=FQ. ∴EP=FQ
拓展延伸
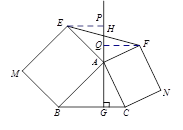 结论: HE=HF.
结论: HE=HF.
理由:过点E作EP⊥GA,FQ⊥GA,垂足分别为P、Q.
∵四边形ABME是矩形,∴∠BAE=90°,
 ∴∠BAG+∠EAP=90°.AG⊥BC,∴∠BAG+∠ABG=90°,
∴∠BAG+∠EAP=90°.AG⊥BC,∴∠BAG+∠ABG=90°,
∴∠ABG=∠EAP.
∵∠AGB=∠EPA=90°,∴△ABG∽△EAP,
同理△ACG∽△FAQ,
∵AB= k AE,AC= kAF,∴EP=FQ.
∵∠EHP=∠FHQ,∴Rt△EPH≌Rt△FQH. ∴HE=HF

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
【题目】下表中给出了变量x与ax2,ax2+bx+c之间的部分对应值(表格中的符号“…”表示该项数据已经丢失)
x | -1 | 0 | 1 |
ax | … | … | 1 |
ax+ bx + c | 7 | 2 | … |
(1)写出这条抛物线的开口方向,顶点D的坐标;并说明它的变化情况;
(2)抛物线![]() 的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
(3)在(2)的条件下,设线段BD交x轴于点C,试写出∠BAD与∠DCO的数量关系,并说明理由.