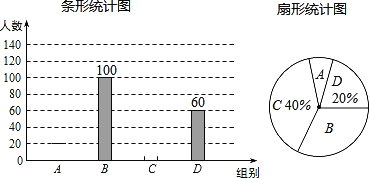
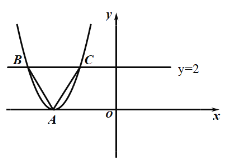题目内容
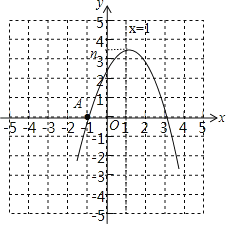
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①2a+b<0;
②﹣1≤a≤﹣![]() ;
;
③对于任意实数m,a(m2﹣1)+b(m﹣1)≤0总成立;
④关于x的方程ax2+bx+c=n+1有两个不相等的实数根.
其中结论正确的序号是_____.
【答案】②③.
【解析】
由对称轴、顶点坐标和y轴交点坐标代入可得b=-2a,c=-3a可判断①②,对函数图像得最大值进行分析可以判断③④.
如图,
∵抛物线的顶点坐标为(1,n),
∴抛物线的对称性为直线x=﹣![]() =1,
=1,
∴b=﹣2a,
∴2a+b=0,所以①错误;
∵抛物线与x轴交于点A(﹣1,0),
∴a﹣b+c=0,
∴c=b﹣a=﹣2a﹣a=﹣3a,
∵抛物线与y轴的交点在(0,2),(0,3)之间(包含端点),
∴2≤c≤3,即2≤﹣3a≤3,
∴﹣1≤a≤﹣![]() ,所以②正确;
,所以②正确;
∵当x=1时,y有最大值,
∴a+b+c≥am2+bm+c(m为任意实数),
即a(m2﹣1)+b(m﹣1)≤0,所以③正确;
∵抛物线的顶点坐标为(1,n),
∴直线y=n与抛物线只有一个交点,
∴直线y=n+1与抛物线没有公共点,
∴关于x的方程ax2+bx+c=n+1没有实数根,所以④错误.
故答案为②③.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
【题目】下表中给出了变量x与ax2,ax2+bx+c之间的部分对应值(表格中的符号“…”表示该项数据已经丢失)
x | -1 | 0 | 1 |
ax | … | … | 1 |
ax+ bx + c | 7 | 2 | … |
(1)写出这条抛物线的开口方向,顶点D的坐标;并说明它的变化情况;
(2)抛物线![]() 的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
(3)在(2)的条件下,设线段BD交x轴于点C,试写出∠BAD与∠DCO的数量关系,并说明理由.