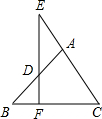题目内容
已知:点O到△ABC的两边AB、AC所在直线的距离OE、OF相等,且OB=OC.
(1)如图,若点O在边BC上,求证:AB=AC;
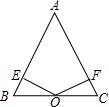
(2)如图,若点O在△ABC的内部,则(1)中的结论还成立吗?若成立,请证明;若不成立,说明理由;
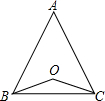
(3)若点O在△ABC的外部,则(1)的结论还成立吗?请画图表示.
(1)如图,若点O在边BC上,求证:AB=AC;

(2)如图,若点O在△ABC的内部,则(1)中的结论还成立吗?若成立,请证明;若不成立,说明理由;

(3)若点O在△ABC的外部,则(1)的结论还成立吗?请画图表示.
(1)证明:∵OE⊥AB,OF⊥AC,
∴∠BEO=∠CFO=90°.
∵在Rt△OBE和Rt△OCF中
,
∴Rt△OBE≌Rt△OCF(HL).
∴∠B=∠C.
∴AB=AC.
(2)成立.
证明:过O作OE⊥AB,OF⊥AC,垂足分别为E、F,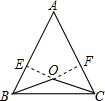
则∠BEO=∠CFO=90°,
∵在Rt△OBE和Rt△OCF中
,
∴Rt△OBE≌Rt△OCF(HL).
∴∠EBO=∠FCO.
∵OB=OC,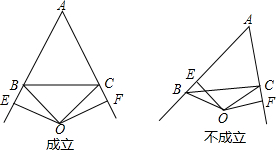
∴∠OBC=∠OCB.
∴∠EBO+∠OBC=∠FCO+∠OCB.
即∠ABC=∠ACB.
∴AB=AC.
(3)不一定成立,如右图.
∴∠BEO=∠CFO=90°.
∵在Rt△OBE和Rt△OCF中
|
∴Rt△OBE≌Rt△OCF(HL).
∴∠B=∠C.
∴AB=AC.
(2)成立.
证明:过O作OE⊥AB,OF⊥AC,垂足分别为E、F,

则∠BEO=∠CFO=90°,
∵在Rt△OBE和Rt△OCF中
|
∴Rt△OBE≌Rt△OCF(HL).
∴∠EBO=∠FCO.
∵OB=OC,

∴∠OBC=∠OCB.
∴∠EBO+∠OBC=∠FCO+∠OCB.
即∠ABC=∠ACB.
∴AB=AC.
(3)不一定成立,如右图.

练习册系列答案
相关题目