题目内容
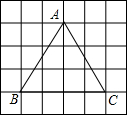
如图,△ABC中,AB=AC,D是AB上一点,DF⊥BC于点F,交CA延长线于点E,求证:AD=AE.
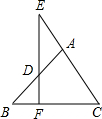
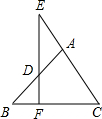
证明:∵△ABC中,AB=AC,
∴∠B=∠C,
∵DF⊥BC,
∴∠E+∠C=90°,∠B+∠BDF=90°,
∴∠E=∠BDF,
∵∠BDF=∠ADE,
∴∠ADE=∠E,
∴AD=AE.
∴∠B=∠C,
∵DF⊥BC,
∴∠E+∠C=90°,∠B+∠BDF=90°,
∴∠E=∠BDF,
∵∠BDF=∠ADE,
∴∠ADE=∠E,
∴AD=AE.

练习册系列答案
相关题目