Question

【题目】D为等边△ABC的边AC上一点，E为直线AB上一点，CD＝BE．

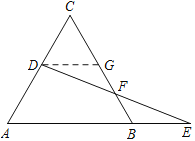
（1）如图1，求证：AD＝DE；

（2）如图2，DE交CB于点F．

①若DE⊥AC，CF＝6，求BF的长；

②求证：DF＝EF．

Answer 1

【答案】（1）证明见解析；（2）①3；②证明见解析

【解析】

（1）根据等边三角形的性质可得AB=AC，∠A=60°，由CD=BE，利用线段的和差关系可得AD=AE，即可证明△ADE是等边三角形，可得AD=DE；（2）①由DE⊥AC可得∠CFD=30°，根据含30°角的直角三角形的性质可求出CD的长，可得BE的长，根据∠BFE＝∠CFD＝30°，∠E＝30°，可得BF=BE，即可得答案；②过点D作DG∥AB，交CB于点G，可得∠CGD＝∠ABC＝60°，∠GDF＝∠E，由∠C=60°可证明△CDG是等边三角形，可得CD=DG，进而可得DG＝BE，利用AAS可证明△GDF≌△BEF，即可得DF=EF.

（1）∵△ABC是等边三角形，

∴AB＝AC，∠A＝60°，

∵CD＝BE，

∴AC=CD=AB-BE，即AD＝AE，

∴△ADE是等边三角形，

∴AD＝DE；

（2）①∵DF⊥AC，

∴∠CDF＝90°，

∵∠C＝60°，

在Rt△CDF中，∠CFD＝30°，

∴CD=CF=×6=3，

∵CD＝BE，

∴BE＝3，

∵∠BFE＝∠CFD＝30°，∠E＝30°，

∴BE＝BF，

∴BF＝3；

②如图，过点D作DG∥AB，交CB于点G，

∴∠CGD＝∠ABC＝60°，∠GDF＝∠E，

∵∠C＝60°，

∴△CDG是等边三角形，

∴CD＝DG，

∵CD＝BE，

∴DG＝BE，

在△GDF和△BEF中，，

∴△GDF≌△BEF（AAS），

∴DF＝EF．