题目内容
【题目】最近雾霾天气频繁,使得空气净化器得以畅销.某商场代理销售某种空气净化器,其进价是500元/台,经过市场销售后发现,当售价是1000元/台时,每月可售出50台,且售价每降低20元,每月就可多售出5台.若供货商规定这种空气净化器售价不能低于600元/台,代理销售商每月要完成不低于60台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式,并求出自变量x的取值范围.
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
【答案】(1)y=300-
(600≤x≤960).(2)当x=850时,w取得最大值,此时w=30625.
【解析】
（1）根据题意可以求得y与x的函数关系式，由供货商规定这种空气净化器售价不能低于600元/台，代理销售商每月要完成不低于60台的销售任务可以求得x的取值范围；
（2）根据题意可以得到w关于x的关系式，然后化为顶点式，从而可以求得w的最大值和此时x的值．
（1）由题意可得，
，
∵货商规定这种空气净化器售价不能低于600元/台，代理销售商每月要完成不低于60台的销售任务，
∴
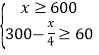
解得，600≤x≤960，
即月销售量y（台）与售价x（元/台）之间的函数关系式是y=300- （600≤x≤960）；
（2）由题意可得，
w=（x-500）（300-）=
，
∴当x=850时，w取得最大值，此时w=30625，
即当售价x定为850元/台时，商场每月销售这种空气净化器所获得的利润w（元）最大，最大利润是30625元．
练习册系列答案
相关题目
