Question

【题目】如图，AB//CD．

（1）如图①，若∠ABE=40o，∠BEC=140o，∠ECD=_________o

（2）如图①，试探究∠ABE，∠BEC，∠ECD的关系，并说明理由；

（3）如图②，若CF平分∠ECD，且满足CF∥BE，试探究∠ECD，∠ABE的数量关系，并说明理由．

Answer 1

【答案】（1）∠ECD=80°；（2）∠BEC=180°-∠ECD+∠ABE；（3）∠ABE=∠ECD．

【解析】

（1）过点E作EF∥AB，根据平行线的性质即可得到∠ECD的度数；

（2）过点E作EF∥AB，根据平行线的性质即可得到∠ABE，∠BEC，∠ECD的关系；

（3）延长BE和DC相交于点G，利用平行线的性质、三角形的外角以及角平分线的性质即可得到答案．

解：

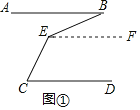
（1）如图①，过点E作EF∥AB，

∵AB∥CD，

∴AB∥EF∥CD，

∴∠ABE=∠BEF，∠FEC+∠ECD=180°，

∵∠ABE=40°，∠BEC=140°，

∴∠FEC=100°，

∴∠ECD=180°-100°=80°；

（2）如图①，过点E作EF∥AB，

∵AB∥CD，

∴AB∥EF∥CD，

∴∠ABE=∠BEF，∠FEC+∠ECD=180°，

∴∠BEC=180°-∠ECD+∠ABE；

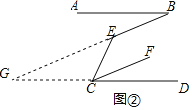
（3）如图②延长BE和DC相交于点G，

∵AB∥CD，

∴∠ABE=∠G，

∵BE∥CF，

∴∠GEC=∠ECF，

∵∠ECD=∠GEC+∠G，

∴∠ECD=∠ECF+∠ABE，

∵CF平分∠ECD，

∴∠ECF=∠DCF，

∴∠ECD=∠ECD+∠ABE，

∴∠ABE=∠ECD．

故答案为：（1）80；（2）∠BEC=180°-∠ECD+∠ABE；（3）∠ABE=∠ECD．