题目内容
【题目】如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有_____个.

【答案】4
【解析】
由A点坐标可得OA=2![]() ,∠AOP=45°,分别讨论OA为腰和底边,求出点P在x轴正半轴和负半轴时,△APO是等腰三角形的P点坐标即可.
,∠AOP=45°,分别讨论OA为腰和底边,求出点P在x轴正半轴和负半轴时,△APO是等腰三角形的P点坐标即可.
(1)当点P在x轴正半轴上,
①如图,以OA为腰时,
∵A的坐标是(2,2),
∴∠AOP=45°,OA=2![]() ,
,
当∠AOP为顶角时,OA=OP=2![]() ,
,
当∠OAP为顶角时,AO=AP,
∴OPA=∠AOP=45°,
∴∠OAP=90°,
∴OP=![]() OA=4,
OA=4,
∴P的坐标是(4,0)或(2![]() ,0).
,0).
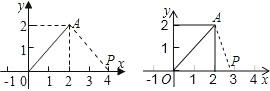
②以OA为底边时,
∵点A的坐标是(2,2),
∴∠AOP=45°,
∵AP=OP,
∴∠OAP=∠AOP=45°,
∴∠OPA=90°,
∴OP=2,
∴P点坐标为(2,0).
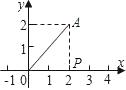
(2)当点P在x轴负半轴上,
③以OA为腰时,
∵A的坐标是(2,2),
∴OA=2![]() ,
,
∴OA=OP=2![]() ,
,
∴P的坐标是(﹣2![]() ,0).
,0).

综上所述:P的坐标是(2,0)或(4,0)或(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).
故答案为:4.

练习册系列答案
相关题目